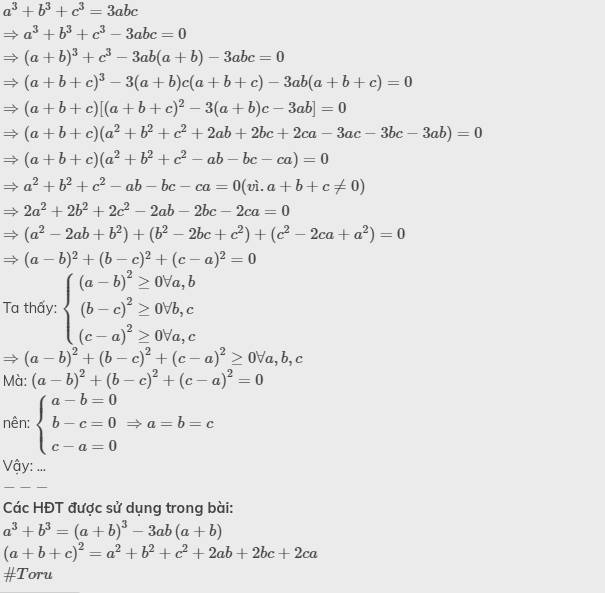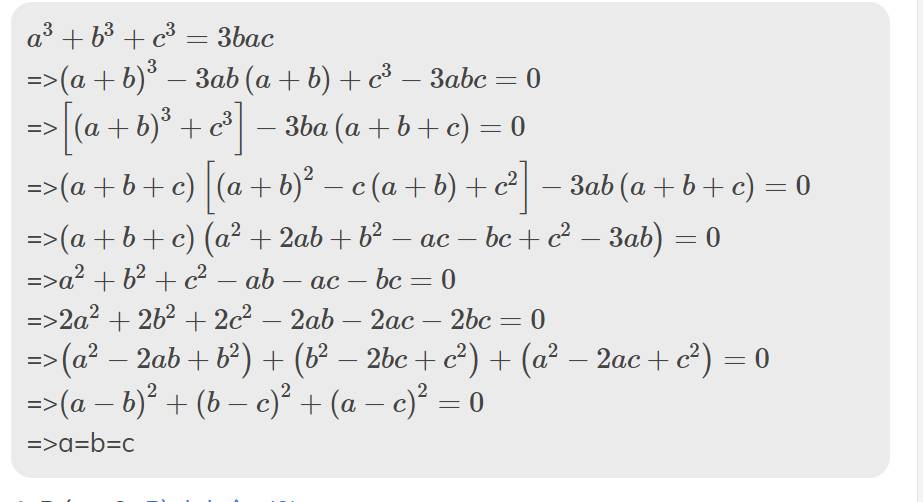Các câu hỏi tương tự
cho \(a^3+b^3+c^3=3abc\) và \(a+b+c\ne0\). C/M \(a=b=c\)
cho \(a+b+c\ne0\) và \(a^3+b^3+c^3=3abc.\)Tính N=\(\frac{a^{2013}+b^{2013}+c^{2013}}{\left(a+b+c^{2013}\right)}\)
Cho a\(a^3+b^3+c^3=3abc\)
Và \(a+b+c\ne0\)
Tính \(A=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
cho \(a^3+b^3+c^3=3abc\)
và \(a+b+c\ne0\)
tính: \(\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Cho \(a^3+b^3+c^3=3abc\) và \(a+b+c\ne0\). Tính giá trị của biểu thức:
\(N=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Cho \(a^3+b^3+c^3=3abc\)
Và \(a+b+c\ne0\)
Tính gia trị biểu thức \(N=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Cho \(a^3+b^3+c^3=3abc\)\(và\)\(a+b+c\ne0\)\(Tính:\)
\(\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Cho \(a^3+b^3+c^3=3abc\) và \(a,b,c\ne0\)
Tính giá trị của biểu thức \(N=\frac{a^2+b^2+c^2}{\left(a+b+a\right)^2}\)
Cho \(a^3+b^3+c^3=3abc\)và \(abc\ne0;a+b+c=0\)
CMR \(\left(\frac{1}{a}+\frac{1}{b}\right)\left(\frac{1}{b}+\frac{1}{c}\right)\left(\frac{1}{c}+\frac{1}{a}\right)=0\)