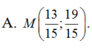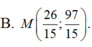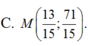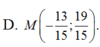Question

Cho A(0;-3) , B(1;3) và đt d: 2x-y-3=0 . Tìm toạ độ điểm M trên d sao cho AM+MB là nhỏ nhất.

Answer 1

Gọi \(M\left(m;2m-3\right)\)

C1:

Khi đó \(\overrightarrow{MA}=\left(-m;-2m\right)\) và \(\overrightarrow{BM}=\left(m-1;2m-6\right)\)

Ta có \(AM+MB=\left|\overrightarrow{MA}\right|+\left|\overrightarrow{BM}\right|\)\(\ge\left|\overrightarrow{MA}+\overrightarrow{BM}\right|\)\(=\sqrt{\left(-m+m-1\right)^2+\left(-2m+2m-6\right)^2}\)\(=\sqrt{37}\)

Đẳng thức xảy ra\(\Leftrightarrow m=0\)

Khi đó, \(M\left(0;-3\right)\)

C2:

Áp dụng BĐT tam giác mở rộng, ta có

 \(AM+MB\ge AB=\sqrt{37}\)

Giải ra cũng tìm được \(M\left(0;-3\right)\) thoả mãn