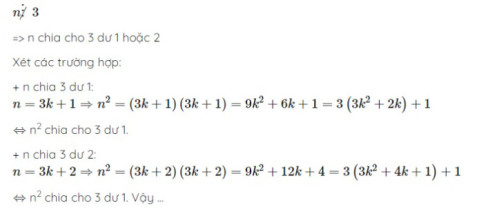Vì \(a⋮̸3\) \(\rightarrow\left[{}\begin{matrix}a=3k+1\\a=3k+2\end{matrix}\right.\) với k tự nhiên.
\(a=3k+1\Rightarrow a^2=\left(3k+1\right)^2\equiv1\left(mod3\right)\)
\(a=3k+2\Rightarrow a^2=\left(3k+2\right)^2=9k^2+12k+4\equiv1\left(mod3\right)\)
Nên ta có đpcm.
Giải:
\(a⋮̸3\)
⇒\(a:3\) (dư 1 hoặc dư 2)
Xét các trường hợp:
+) \(a:3\) (dư 1)
\(a=3k+1\)
\(\Rightarrow a^2=\left(3k+1\right).\left(3k+1\right)=9k^2+6k+1=3.\left(3k^2+2k\right)+1\)
\(\Leftrightarrow a^2:3\) (dư 1)
+) \(a:3\) (dư 2)
\(a=3k+2\)
\(\Rightarrow a^2=\left(3k+2\right).\left(3k+2\right)=9k^2+12k+4=3.\left(3k^2+4k+1\right)+1\)
\(\Leftrightarrow a^2:3\) (dư 1)
Vậy \(a^2:3\) (dư 1)