Phương pháp: Cho a = 1, tính tính phân bằng máy tính và so sánh với các đáp án
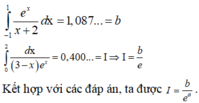
Chọn B
Phương pháp: Cho a = 1, tính tính phân bằng máy tính và so sánh với các đáp án
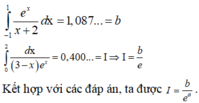
Chọn B
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho số thực a ≠ 0 . Đặt b = ∫ - a a 1 ( 2 a + x ) . e x d x . Tính I = ∫ 0 2 a e x 3 a - x d x theo a và b.
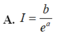
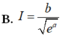
![]()
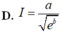
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và f(x)>0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và 2 đường thẳng x=a; x=b Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
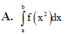
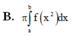
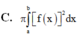
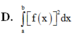
Câu 1. Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số
A. y = -2
B. y = -1
C. x = 2
D. y = 2
Câu 2. Cho hàm số f(x) = x2lnx. Tính f'(e)
A. 3e
B. 2e
C. e
D. 2 + e
Câu 3. Viết công thức tính V của khối cầu có bán kính r.
Câu 4. Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất?
A. 48
B. 46
C. 52
D. 51
Câu 5. Tìm tập xác định D của hàm số y = ln(x2 - 3x)
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Cho hai hàm số F ( x ) = ( x 2 + a x + b ) e - x và f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a = 1 b = -7
B. a = -1 b = -7
C. a = -1 b = 7
D. a = 1 b = 7
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a;x=b (a,b)Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức

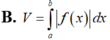
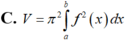
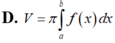
Cho hàm số y =f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = f)x), trục hoành và hai đường thẳng x=a; x=b (a<b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
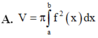
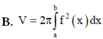
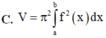

Cho các số thực a, b khác không. Xét hàm số f x = a x + 1 3 + b x e x với mọi x khác –1. Biết f’(0) = –22 và ∫ 0 1 f x d x = 5 . Tính a + b?
A. 19.
B. 7.
C. 8.
D. 10.
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x = a; x = b Diện tích S của hình phẳng D được tính theo công thức
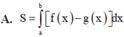
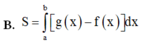
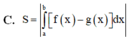
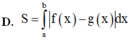
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()