Chọn D
Ta có
f ' x = - 3 a x + 1 4 + b e x + b x e x
nên f’(0) = x – 3a + b = –22 (1).
Xét
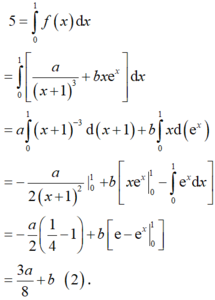
Từ (1) và (2) ta có
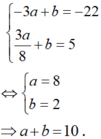
Chọn D
Ta có
f ' x = - 3 a x + 1 4 + b e x + b x e x
nên f’(0) = x – 3a + b = –22 (1).
Xét
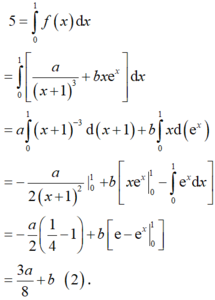
Từ (1) và (2) ta có
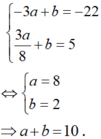
Cho hàm số f ( x ) = a ( x + 1 ) 3 + b x e x . Tìm a và b biết rằng f'(0) = -22 và ∫ 0 1 f ( x ) d x = 5
A. a = -2; b = -8
B. a = 2; b = 8
C. a = 8; b = 2
D. a = -8; b = -2
Cho hàm số f(x) xác định và có đạo hàm f'(x) liên tục trên đoạn [1;3], f x ≠ 0 với mọi x ∈ 1 ; 3 , đồng thời f ' x 1 + f x 2 = f x 2 x - 1 2 và f(1) = -1
Biết rằng ∫ 1 3 f x d x = a ln 3 + b , a , b ∈ Z , tính tổng S = a + b 2
A. S = 0
B. S = -1
C. S = 2
D. S = 4
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x ; f ( 1 ) = ln 1 2 Biết ∫ 1 2 x 2 + 1 f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27/2
B. 1/6
C. 7/6
D. -3/2
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho hàm số f(x) liên tục và a>0. Giả sử với mọi x ∈ 0 ; a ta có f(x)>0 và f(x).f(a-x) = 1. Tính I = ∫ 0 a d x 1 + f ( x )
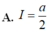
![]()
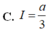
![]()
hàm số f(x)xác định trên tập số thực thỏa mãn hệ thức :f(x+1)=2f(x).Biết rằng với mọi x\(\in\)(0,1)thì f(x)=x(x-1)còn với mọi x \((\in-\infty,,m)\)
thì f(x)\(\ge\)-8/9
xác định giá trị của m từ các phương án sau đây:
A.9/4 B.7/3 C.5/2 D.8/3
giải giúp mik nha <3
Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi x ∈ 0 ; a , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính I = ∫ 0 a d x 1 + f ( x ) .
A. a 2 .
B. 2a.
C. a 3 .
D. aln(a + 1).