Chọn C.
Do a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi b – a = c – b
⇔ (b – a)2 = (c – b)2 ⇔ a2 – c2 = 2ab – 2bc
⇔ a2 +c2 = 2c2 + 2ab – 2bc = 2ab + 2c(c – b) = 2ab + 2c(b – a) = 2ab + 2bc – 2ac.
Chứng minh rằng nếu các số a 2 , b 2 , c 2 lập thành một cấp số cộng a , b , c ≠ 0 thì các số 1 / b + c , 1 / c + a , 1 / a + b cũng lập thành một cấp số cộng.
Cho tam giác ABC. Với tan A 2 ,tan B 2 ,tan C 2 lập thành cấp số cộng nếu và chỉ nếu
A. sinA; sinB; sinC lập thành cấp số cộng.
B. sinA; sinB; sinC lập thành cấp số nhân
C. cosA; cosB; cosC lập thành cấp số cộng.
D. cosA; cosB; cosC lập thành cấp số nhân.
Xét ba số thực a;b;c thay đổi thuộc đoạn [0;3]. Giá trị lớn nhất của biểu thức T = 4 ( a - b ) ( b - c ) ( c - a ) ( a b + b c + c a ) - ( a 2 + b 2 + c 2 ) là
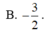
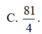
Cho a và b là các số thực. Biết lim x → ∞ ( a x + b - x 2 - 6 x + 2 ) = 3 thì tổng 2ab+b+ a 2 bằng
A.1
B.-6
C.7
D.-5
Để a và b là số thực. Biết lim x → + ∞ ( a x + b - x 2 - 6 x + 2 = 3 thì tổng 2 a b + b + a 2 bằng
A. 1
B. -6
C. 7
D. -5
Cho a, b, c là các số thực, theo thứ tự lập thành cấp số nhân.
Biết a + b + c = 26 a 2 + b 2 + c 2 = 364 Tìm b.
A. 9
B. 7
C. 6
D. 5
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. AD=2BC, AB=BC=a, SA vuông góc với đáy, SA= a 2 . Tính góc giữa (AC, (SCD)).
Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. a 2 + c 2 = 2 a b + 2 b c + 2 a c
B. a 2 − c 2 = 2 a b + 2 b c − 2 a c
C. a 2 + c 2 = 2 a b + 2 b c − 2 a c
D. a 2 − c 2 = 2 a b − 2 b c + 2 a c
Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. a 2 + c 2 = 2 a b + 2 b c
B. a 2 − c 2 = 2 a b − 2 b c
C. a 2 + c 2 = 2 a b − 2 b c
D. a 2 − c 2 = a b − b c
