Đáp án A
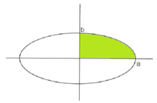
Xét hình phẳng D giới hạn bởi các trục Ox, Oy và đồ thị của hàm số 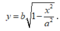
Diện tích elip bằng 4 lần diện tích hình phẳng D.
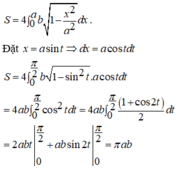
Đáp án A

Xét hình phẳng D giới hạn bởi các trục Ox, Oy và đồ thị của hàm số 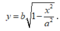
Diện tích elip bằng 4 lần diện tích hình phẳng D.
Cho a > b > 0 . Đường elip (E) có phương trình x 2 a 2 + y 2 b 2 = 1 . Diện tích của hình elip (E) là
A. a 2 + b 2 2 π
B. 2 πab
C. 4 πab
D. πab
Thể tích khối vật thể tròn xoay khi quay hình phẳng (S) giới hạn bởi các đường y = 1 - x 2 , y = 0 quanh trục hoành có kết quả dạng π a b với a b là phân số tối giản. Khi đó a+b bằng:
A. 31
B. 23
C. 21
D. 32
Cho hình phẳng (H) giới hạn bởi đường cong C : y = x 3 - 3 x + 2 và P : y = 2 x + 2 . Thể tích của khối tròn xoay nhận được khi cho (H) quay quanh trục Ox có dạng V = πa b + 2018 c + 2019 d . Hỏi mệnh đề nào trong các mệnh đề sau là sai?
A. abcd = 0
B. 9a - b - c - d = 1
C. a + b + 2 c + 3 d = 39
D. b + d a + c + 1 = 8
Cho elip (E) có phương trình x²/16 + y²/9 =1. Viết phương trình đường thẳng (d) đi qua M(1;2) và cắt (E) tại A, B sao cho M là trung điểm AB
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 ( v ớ i - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
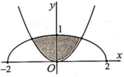
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z - 2 + z + 2 = 6 là đường elip E . Phương trình đường elip E là
A. x 2 5 + y 2 4 = 1
B. x 2 9 + y 2 5 = 1
C. x 2 9 + y 2 4 = 1
D. x 2 36 + y 2 5 = 1
Trong mặt phẳng O x y , cho điểm C 3 ; 0 và elip E : x 2 9 + y 2 1 = 1 . A , B là 2 điểm thuộc E sao cho ∆ A B C đều, biết tọa độ của A a 2 ; c 3 2 và A có tung độ âm. Khi đó a + c bằng:
A. 2
B. 0
C. -2
D. -4
Đường cong parabol y = x 2 6 chia đường elip (E) có độ dài trục lớn và trục bé lần lượt bằng 4 và 2 thành hai phần có tỉ số diện tích bằng (tham khảo hình vẽ bên)
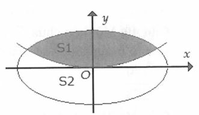
A. S 1 S 2 = 2 3 5
B. S 1 S 2 = 2 π + 3 4 π - 3
C. S 1 S 2 = 4 π + 3 8 π - 3
D. S 1 S 2 = 3 2
Trong không gian Oxyz cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 27 . Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0;-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng ( α ) có phương trình dạng ax+by-z+c= 0, khi đó a-b+c bằng:
A. -4.
B. 8
C. 0
D. 2