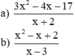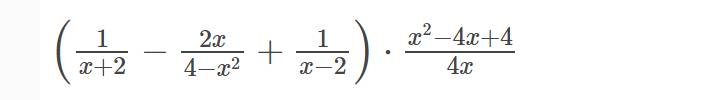Đề bài bạn viết hơi khó hiểu, nhưng có thể tạm giải như sau:
Lời giải:
$A=\frac{4x^2}{x+1}=\frac{4(x^2-1)+4}{x+1}=\frac{4(x-1)(x+1)+4}{x+1}$
$=4(x-1)+\frac{4}{x+1}$
Với $x$ nguyên thì:
$A\in\mathbb{Z}\Leftrightarrow 4(x-1)+\frac{4}{x+1}\in\mathbb{Z}$
$\Leftrightarrow \frac{4}{x+1}\in\mathbb{Z}$
$\Leftrightarrow x+1$ là ước của $4$
$\Rightarrow x+1\in\left\{\pm 1;\pm 2;\pm 4\right\}$
$\Rightarrow x\in\left\{-2; 0; -3; 1; 3; -5\right\}$