Câu 29. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).Câu 30. Cho a3 + b3 2. Chứng minh rằng a + b ≤ 2.Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].Câu 32. Tìm giá trị lớn nhất của biểu thức: Câu 33. Tìm giá trị nhỏ nhất của: với x, y, z 0.Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:a) ab và a/b là số vô tỉ.b) a + b và a/b là số hữu tỉ (a + b ≠ 0)c) a + b, a2 và b2 là số hữu tỉ (a + b ≠...
Đọc tiếp
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: 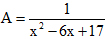
Câu 33. Tìm giá trị nhỏ nhất của: 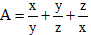 với x, y, z > 0.
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
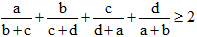
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
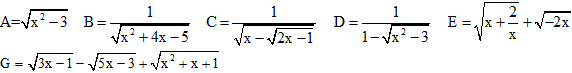 Mn giúp em với ;-;
Mn giúp em với ;-;








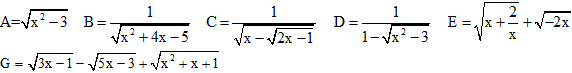 Mn giúp em với ;-;
Mn giúp em với ;-;




