Chọn D.
Do 2 vecto ![]() là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
![]() nên
nên ![]()
Suy ra:
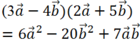
= 6.1- 20.1+ 7.1= - 7.
Chọn D.
Do 2 vecto ![]() là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
là 2 vecto đơn vị nên độ dài mỗi vecto là 1.
![]() nên
nên ![]()
Suy ra:
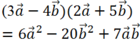
= 6.1- 20.1+ 7.1= - 7.
Cho hai vectơ a → ; b → thỏa mãn a → = 3 , b → = 2 và a → b → = - 3 . Xác định góc giữa hai vectơ đó
A. 300
B. 600
C. 1350
D. 1200
Cho hai vectơ a → và b → thỏa mãn a → = 3, b → = 2 và a → . b → = − 3. Xác định góc α giữa hai vectơ a → và b →
A. α = 30 0 .
B. α = 45 0 .
C. α = 60 0 .
D. α = 120 0 .
Cho hai vectơ a → và b → thỏa mãn a → = 3, b → = 2 và a → . b → = − 3. Xác định góc α giữa hai vectơ a → và b →
A. α = 30 0 .
B. α = 45 0 .
C. α = 60 0 .
D. α = 120 0 .
[1] Cho hai tập hợp A = { 1; 2; 3; 4; 5 }; B = { 4; 5; 6; 7 }. Xác định tập hợp T = A \ B
T = { 1; 2; 3 } B. T = { 4; 5} C. T = { 6; 7 } D. T = { 1; 2; 3; 4; 5; 6; 7 }
[1] Cho hai tập hợp A = { 1; 2; 3; 4; 5 }; B = { 3; 4; 5 }. Biết B \(\subset A\), xác định tập hợp T = \(C_AB\)
A. T = { 1; 2; 3 } B. T = { 3; 4: 5 } C. T = { 1; 2 } D. T = { 1; 2; 3; 4; 5 }
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Cho vectơ a = (2; -2), vectơ b = (1; 4). Hãy phân tích vectơ c (5; 0) theo hai vectơ a và b.
Cho các vectơ a → ( 1 ; 3 ) ; b → ( 2 ; 5 ) ; c → ( 7 ; 19 ) . Phân tích vectơ c → theo các vectơ a → ; b → là:
A. c → = 3 a → + 2 b →
B. c → = 3 a → - 2 b →
C. c → = 2 a → + 3 b →
D. c → = 2 a → - 3 b →
Cho hai vectơ a → ; b → thỏa mãn a → = 4 , b → = 5 , a → , b → = 120 ° . Giá trị của tích vô hướng a → . b → là:
A. 10
B. -10
C. 10 3
D. - 10 3