Cho 2 đường thẳng
(d₁): y = \(\left(2+m\right)x+1\:\:\left(m\ne-2\right)\)
(d₂): y = \(\left(1+2m\right)x+2\:\left(m\ne-\dfrac{1}{2}\right)\)
a) Tìm m để (d₁) và (d₂) cắt nhau.
b) Với m = -1, vẽ (d₁) và (d₂) trên cùng một mặt phẳng tọa độ Oxy rồi tìm tọa độ giao điểm của 2 đường thẳng đó.
c) Tìm khoảng cách lớn nhất từ A(1;3) đến (d₁).
a: Để (d1) và (d2) cắt nhau thì \(2m+1\ne m+2\)
=>\(2m-m\ne2-1\)
=>\(m\ne1\)
b: Khi m=-1 thì (d1): \(y=\left(2-1\right)x+1=x+1\)
Khi m=-1 thì (d2): \(y=\left(1-2\right)x+2=-x+2\)
Vẽ đồ thị:
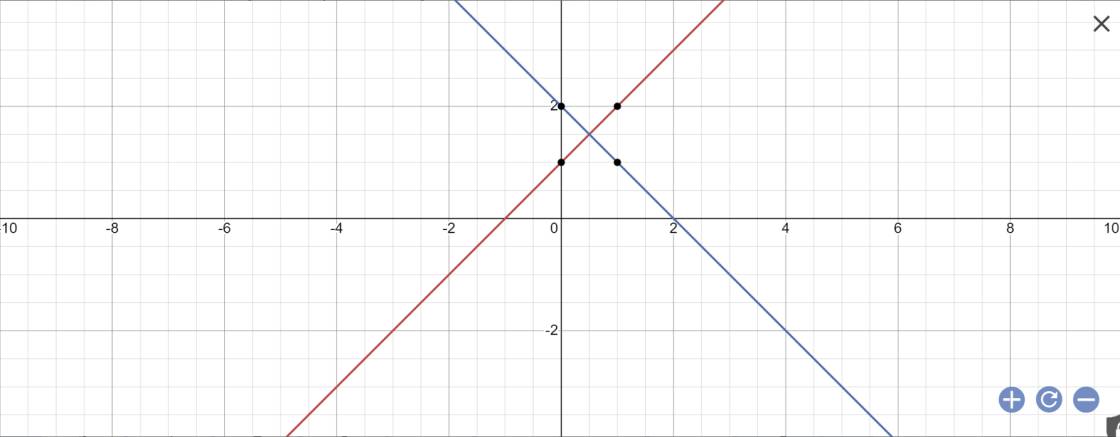
Phương trình hoành độ giao điểm là:
x+1=-x+2
=>x+x=2-1
=>2x=1
=>\(x=\dfrac{1}{2}\)
Thay x=1/2 vào y=x+1, ta được:
\(y=\dfrac{1}{2}+1=\dfrac{3}{2}\)
c:
(d1): y=(m+2)x+1
=>(m+2)x-y+1=0
Khoảng cách từ A(1;3) đến (d1) là:
\(d\left(A;\left(d1\right)\right)=\dfrac{\left|1\left(m+2\right)+3\cdot\left(-1\right)+1\right|}{\sqrt{\left(m+2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|m\right|}{\sqrt{\left(m+2\right)^2+1}}\)
Để d(A;(d1)) lớn nhất thì m+2=0
=>m=-2
Vậy: \(d\left(A;\left(d1\right)\right)_{max}=\dfrac{\left|-2\right|}{\sqrt{\left(-2+2\right)^2+1}}=\dfrac{2}{1}=2\)














