Question

đúng sai nhé mn

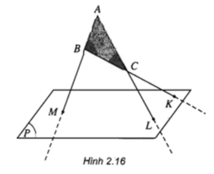
Câu 6: Cho hình bình hành \(ABCD\) và \(ABEF\) nằm ở hai mặt phẳng khác nhau. Gọi \(M\) là trọng tâm \(\Delta ABE\). Gọi \((P)\) là mặt phẳng đi qua \(M\) và song song với mặt \((ADF)\). Gọi \(N\) là giao điểm của \((P)\) và \(AC\). Xét tính đúng sai của các khẳng định sau:

a) \(EFDC\) là hình thang

b) \(FD \parallel EC\)

c) \((ADF) \parallel (BCE)\)

d) \(\frac{AN}{NC} = 3\)

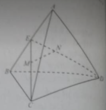
Câu 7: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(M, N\) lần lượt là trung điểm của \(SA\) và \(SD\). Xét tính đúng sai của các khẳng định sau:

a) \(ON\) chéo nhau với \(SB\)

b) \((OMN) \parallel (SBC)\)

c) Gọi \(P\) và \(Q\) là trung điểm của \(AB\) và \(ON\). Khi đó \(PQ\) cắt \((SBC)\)

d) Gọi \(R\) là trung điểm \(AD\). Khi đó \((MOR) \parallel (SCD)\)

Answer 1

Câu 7:

a: ABCD là hình bình hành tâm O

=>O là trung điểm chung của AC và BD

Xét ΔDBS có O,N lần lượt là trung điểm của DB,DS

=>ON là đường trung bình của ΔDBS

=>ON//SB

=>Sai

b: xét ΔSAC có O,M lần lượt là trung điểm của AC,AS

=>OM là đường trung bình của ΔSAC

=>OM//SC

=>OM//(SBC)

ON//SB

=>ON//(SBC)

mà OM//(SBC)

và ON,OM cùng thuộc mp(OMN)

nên (OMN)//(SBC)

=>Đúng

d: Xét ΔSAD có M,R lần lượt là trung điểm của AS,AD

=>MR là đường trung bình của ΔSAD

=>MR//SD

=>MR//(SCD)

MO//SC

=>MO//(SCD)

mà MR//(SCD) và MO,MR cùng thuộc mp(MOR)

nên (MOR)//(SCD)

=>Đúng