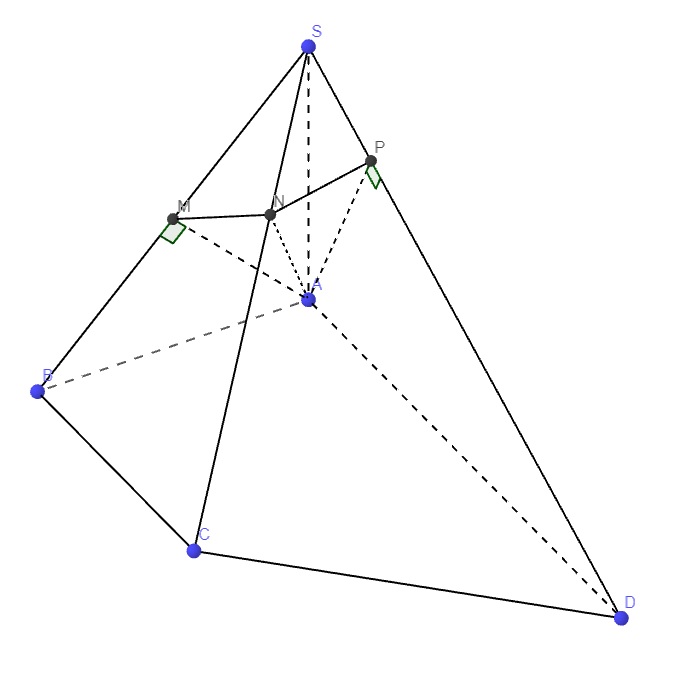
a.
Hiển nhiên câu này sai rồi (nếu SA vuông SD đồng nghĩa SD song song AD, vô lý do chúng đã cắt nhau tại D)
b.
Câu này đúng. SA vuông góc (ABCD) nên SA vuông góc AB
c.
Câu này sau, góc giữa SD và BC bằng góc giữa SD và AD (do AD song song BC), chính là góc SDA
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{1}{2}\) nên nó chỉ khoảng 26 độ thôi
d.
Hệ thức lượng:
\(AM=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{2}}{2}\)
\(AN=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{6}}{3}\)
\(AP=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\dfrac{2a\sqrt{5}}{5}\)
Tam giác AMN vuông tại M (do BC vuông (SAB) nên AM vuông (SBC) => AM vuông MN)
\(MN=\sqrt{AN^2-AM^2}=\dfrac{a\sqrt{6}}{6}\)
\(\Rightarrow S_{AMN}=\dfrac{1}{2}AM.MN=\dfrac{a^2\sqrt{3}}{12}\)
Tam giác ANP vuông tại N (do AN vuông góc (SCD))
\(NP=\sqrt{AP^2-AN^2}=\dfrac{a\sqrt{30}}{15}\)
\(S_{ANP}=\dfrac{1}{2}AN.AP=\dfrac{a^2\sqrt{5}}{15}\)
\(\Rightarrow S_{AMN}+S_{ANP}=a^2\left(\dfrac{\sqrt{3}}{12}+\dfrac{\sqrt{5}}{15}\right)\) ko có dạng như đáp án