Các câu hỏi tương tự
Câu 4: Cho ΔABC, điểm O ở bên trong tam giác. Gọi theo thứ tự là trung điểm của OA, OB, OC.
a) Chứng minh rằng ΔABC đồng dạng với ΔMNP.
b) Tính chu vi của ΔMNP biết chu vi của ΔABC bằng 88cm.
Câu 4: Cho ΔABC, điểm O ở bên trong tam giác. Gọi theo thứ tự là trung điểm của OA, OB, OC.
a) Chứng minh rằng ΔABC đồng dạng với ΔMNP.
b) Tính chu vi của ΔMNP biết chu vi của ΔABC bằng 88cm.
Cho điểm O nằm trong ΔABC. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a. Chứng minh: ΔPQR đồng dạng ΔABC b. Tính chu vi ΔPQR, biết chu vi ΔABC bằng 540 cm.
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.a) Chứng minh
Δ
P
Q
R
∽
Δ
A
B
C
.b) Cho biết
Δ
A
B
C
có chu vi bằng 543cm, hãy tính chu vi
Δ
P
Q
R
.
Đọc tiếp
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a) Chứng minh Δ P Q R ∽ Δ A B C .
b) Cho biết Δ A B C có chu vi bằng 543cm, hãy tính chu vi Δ P Q R .
Cho ΔABC và ΔMNP đồng dạng với nhau theo tỉ số đồng dạng k = 3/2 . Chu vi tam giác ABC bằng 36cm. Chu vi tam giác MNP là:
A. 24cm
B. 54cm
C. 18cm
D. 12cm
Cho ΔABC, gọi D, E theo thứ tự là trung điểm của AB, AC. Gọi O là điểm bất kì nằm trong ΔABC. Vẽ điểm M đối xứng O qua D, vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành Cho ΔABC, gọi D, E theo thứ tự là trung điểm của AB, AC. Gọi O là điểm bất kì nằm trong ΔABC. Vẽ điểm M đối xứng O qua D, vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành
Đọc tiếp
Cho ΔABC, gọi D, E theo thứ tự là trung điểm của AB, AC. Gọi O là điểm bất kì nằm trong ΔABC. Vẽ điểm M đối xứng O qua D, vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành Cho ΔABC, gọi D, E theo thứ tự là trung điểm của AB, AC. Gọi O là điểm bất kì nằm trong ΔABC. Vẽ điểm M đối xứng O qua D, vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành
ΔA'B'C' 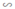 ΔABC theo tỉ số đồng dạng k = 3/5.
ΔABC theo tỉ số đồng dạng k = 3/5.
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết hiệu chu vi của hai tam giác là 40dm, tính chu vi của mỗi tam giác.
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...b) Nếu
Δ
A
B
C
~
Δ
D
E
F
với tỉ số đồng dạng là 1/2 và
Δ
D
E
F
~
Δ
M
N
P
với tỉ số đồng dạng là 4/3 thì
Δ
M
N
P...
Đọc tiếp
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu Δ A B C ~ Δ D E F với tỉ số đồng dạng là 1/2 và Δ D E F ~ Δ M N P với tỉ số đồng dạng là 4/3 thì Δ M N P ~ Δ A B C với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho A I / A B = A K / B C t h ì I K / / B C . . . .
d) Hai tam giác đồng dạng thì bằng nhau....
cho ΔABC đồng dạng ΔHIK theo tỉ số đồng dạng k=7/3. Tính chu vi mỗi tam giác biết hiệu chu vi 2 tam giác là 48cm






