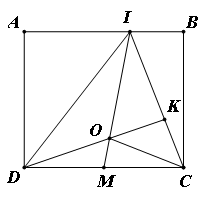
Câu 16 . Cho hình vuông ABCD có cạnh dài 6cm. Trên cạnh AB lấy điểm I sao cho AI = \(\dfrac{2}{3}\) AB.
a) Tính diện tích tứ giác AICD.
b) Trên đoạn thẳng IC lấy điểm K sao cho KC = \(\dfrac{1}{2}\) KI. Tính diện tích tam giác DKC.
c) Gọi M là điểm chính giữa cạnh CD, IM cắt KD tại O. So sánh hai đoạn thẳng OK và OD.
Đề ôn vào lớp 6( chọn)
a) \(S_{ABCD}=6.6=36\left(cm^2\right)\)
\(S_{ABC}=\dfrac{S_{ABCD}}{2}=\dfrac{36}{2}=18\left(cm^2\right)\)
\(AI+BI=AB;AI=\dfrac{2}{3}AB\)
\(\Rightarrow\dfrac{2}{3}AB+BI=AB\Rightarrow BI=\dfrac{1}{3}AB\)
\(\dfrac{S_{IBC}}{S_{ABC}}=\dfrac{IB}{AB}=\dfrac{1}{3}\Rightarrow S_{IBC}=\dfrac{S_{ABC}}{3}=\dfrac{18}{3}=6\left(cm^2\right)\)
\(S_{AICD}=S_{ABCD}-S_{IBC}=36-6=30\left(cm^2\right)\)
b) △DCI có: BC là đường cao, DC là đáy ứng với đường cao BC.
\(\Rightarrow S_{DCI}=\dfrac{1}{2}BC.DC=\dfrac{1}{2}.6.6=18\left(cm^2\right)\)
\(KI=2KC;KC+KI=IC\)
\(\Rightarrow KC+2KC=IC\Rightarrow KC=\dfrac{1}{3}IC\)
\(\dfrac{S_{DKC}}{S_{DCI}}=\dfrac{KC}{IC}=\dfrac{1}{3}\Rightarrow S_{DKC}=\dfrac{1}{3}S_{DCI}=\dfrac{1}{3}.18=6\left(cm^2\right)\)
c) Xét △IDM và △ICM có cùng đường cao và 2 đáy bằng nhau.
\(\Rightarrow S_{IDM}=S_{ICM}\left(1\right)\).
Tương tự \(S_{ODM}=S_{OCM}\left(2\right)\)
Lấy (1)-(2) ta có: \(S_{ODI}=S_{OCI}\)
Mà \(S_{OCI}>S_{OIK}\Rightarrow S_{ODI}>S_{OIK}\)
Mặt khác 2 tam giác này có cùng đường cao.
\(\Rightarrow OD>OK\)
mình lm trong word vì mik ko bt để chữ trong khung