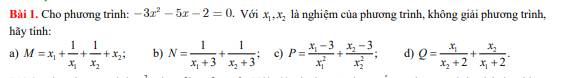1) Khi \(x=9\Rightarrow B=\dfrac{\sqrt{9}-5}{\sqrt{9}+2}=\dfrac{3-5}{3+2}=-\dfrac{2}{5}\)
2) \(...\Rightarrow A=\dfrac{x+3\sqrt{x}+\sqrt{x}-5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{x+4\sqrt{x}+4-9}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\dfrac{\left(\sqrt{x}+2\right)^2-9}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-5}\)
\(\Rightarrow P=A.B=\dfrac{\sqrt{x}-1}{\sqrt{x}-5}.\dfrac{\sqrt{x}-5}{\sqrt{x}+2}=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
3) \(P>\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+2}>\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}-3>\sqrt{x}+2\)
\(\Leftrightarrow2\sqrt{x}>5\)
\(\Leftrightarrow\sqrt{x}>\dfrac{5}{2}\)
\(\Leftrightarrow x>\dfrac{25}{4}\)