Các câu hỏi tương tự
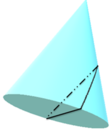
Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng
α
qua tâm đáy và tạo với mặt đáy một góc
60
°
tính tỷ số thể tích của hai phần khối nón chia bởi mặt phẳng
α
?
Đọc tiếp
Cắt một khối nón tròn xoay có bán kính đáy bằng R, đường sinh 2R bởi một mặt phẳng α qua tâm đáy và tạo với mặt đáy một góc 60 ° tính tỷ số thể tích của hai phần khối nón chia bởi mặt phẳng α ?
![]()
![]()
![]()
![]()
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
Cho một khối nón có bán kính đáy là 9cm, góc giữa đường sinh và mặt đáy là
30
0
. Tính diện tích thiết diện của khối nón cắt bởi mặt phẳng đi qua hai đường sinh vuông góc với nhau.
Đọc tiếp
Cho một khối nón có bán kính đáy là 9cm, góc giữa đường sinh và mặt đáy là 30 0 . Tính diện tích thiết diện của khối nón cắt bởi mặt phẳng đi qua hai đường sinh vuông góc với nhau.
![]()
![]()
![]()
![]()
Cho hình nón (N) có đường sinh tạo với đáy một góc
60
0
. Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể tích V của khối nón giới hạn bởi (N).
Đọc tiếp
Cho hình nón (N) có đường sinh tạo với đáy một góc 60 0 . Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể tích V của khối nón giới hạn bởi (N).
![]()
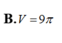
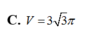
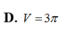
Cho hình nón có đỉnh S, đáy là đường tròn tâm O sao cho SO
a
5
, một mặt phẳng
α
cắt mặt nón theo hai đường sinh SA, SB. Biết khoảng cách từ O đến mặt phẳng
α
bằng
2
5
và diện tích tam giác SAB bằng 360. Thể tích khối nón bằng:
Đọc tiếp
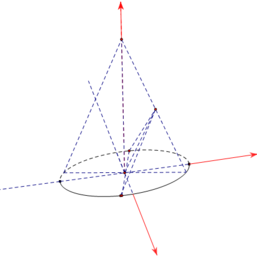
Cho hình nón có đỉnh S, đáy là đường tròn tâm O sao cho SO= a 5 , một mặt phẳng α cắt mặt nón theo hai đường sinh SA, SB. Biết khoảng cách từ O đến mặt phẳng α bằng 2 5 và diện tích tam giác SAB bằng 360. Thể tích khối nón bằng:
![]()
![]()
![]()
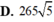
Một khối nón có bán kính đáy bằng 2cm, chiều cao bằng
3
cm. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc
60
°
chia khối nón làm 2 phần. Tính thể tích V phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
Đọc tiếp
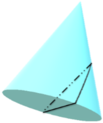
Một khối nón có bán kính đáy bằng 2cm, chiều cao bằng 3 cm. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc 60 ° chia khối nón làm 2 phần. Tính thể tích V phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
![]()
![]()
![]()
![]()
Khối cầu (S) có tâm, đường kính AB 2R. Cắt (S) bởi một mặt phẳng vuông góc với đường kính AB ta được thiết diện là hình tròn (C) rồi bỏ đi phần lớn hơn. Tính thể tích phần còn lại theo R, biết hình nón đỉnh I và đáy là hình tròn (C) có góc ở đỉnh bằng
120
∘
Đọc tiếp
Khối cầu (S) có tâm, đường kính AB = 2R. Cắt (S) bởi một mặt phẳng vuông góc với đường kính AB ta được thiết diện là hình tròn (C) rồi bỏ đi phần lớn hơn. Tính thể tích phần còn lại theo R, biết hình nón đỉnh I và đáy là hình tròn (C) có góc ở đỉnh bằng 120 ∘
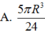
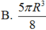
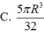
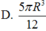
Khối cầu (S) có tâm, đường kính AB2R. Cắt (S) bởi một mặt phẳng vuông góc với đường kính AB ta được thiết diện là hình tròn (C) rồi bỏ đi phần lớn hơn. Tính thể tích phần còn lại theo R, biết hình nón đỉnh I và đáy là hình tròn (C) có góc ở đỉnh bằng
120
°
.
Đọc tiếp
Khối cầu (S) có tâm, đường kính AB=2R. Cắt (S) bởi một mặt phẳng vuông góc với đường kính AB ta được thiết diện là hình tròn (C) rồi bỏ đi phần lớn hơn. Tính thể tích phần còn lại theo R, biết hình nón đỉnh I và đáy là hình tròn (C) có góc ở đỉnh bằng 120 ° .
![]()
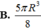
![]()
![]()
Cho khối nón tròn xoay có đường cao h 20 cm, bán kính đáy r 25 cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng: A. 500
c
m
2
B. 475
c
m
2
C. 450
c
m
2
D. 550...
Đọc tiếp
Cho khối nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng:
A. 500 c m 2
B. 475 c m 2
C. 450 c m 2
D. 550 c m 2