Người thứ 3 gieo được \(3\cdot3=3^2\left(hạt\right)\)
Người thứ 4 gieo được \(3^2\cdot3=3^3\left(hạt\right)\)
...
Người thứ 102 gieo được: \(3^{100}\cdot3=3^{101}\left(hạt\right)\)
Tổng số hạt gieo được là:
\(A=3^0+3+3^2+...+3^{101}\)
\(=\left(1+3+3^2\right)+...+\left(3^{99}+3^{100}+3^{101}\right)\)
\(=13+3^3\cdot13+...+3^{99}\left(1+3+3^2\right)\)
\(=13\cdot\left(1+3^3+...+3^{99}\right)⋮13\)





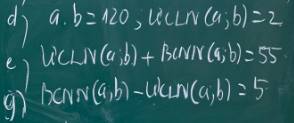

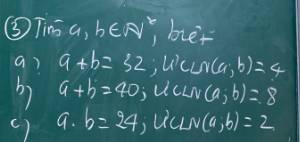
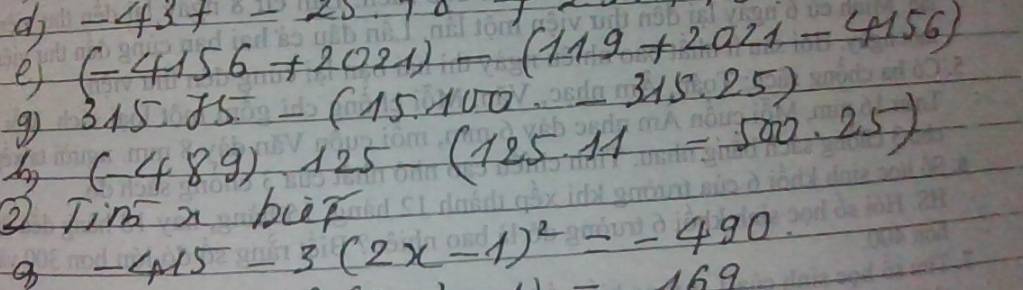

 chỉ giúp em mấy bài này với ạ em đng cần gấp ạ
chỉ giúp em mấy bài này với ạ em đng cần gấp ạ
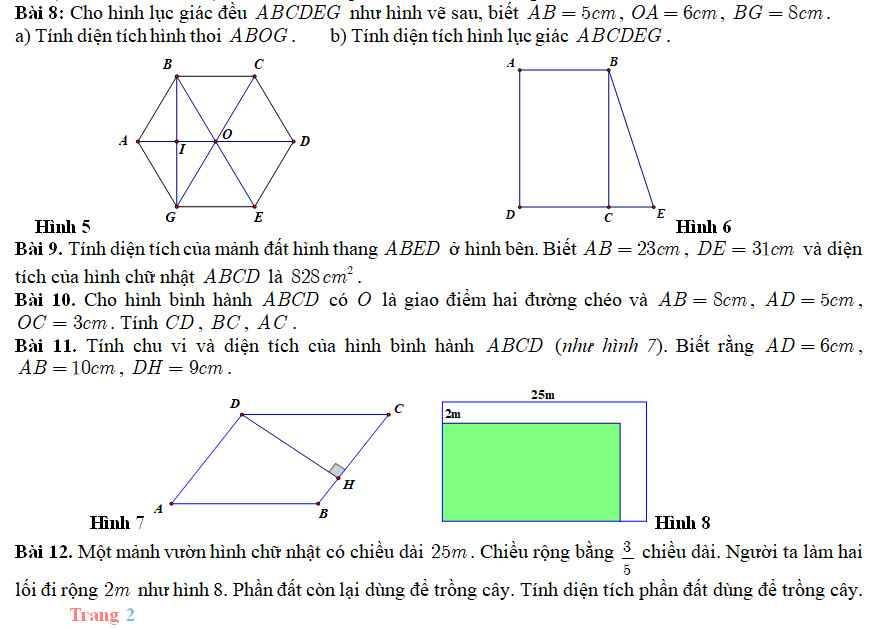
 Giúp mình bài này với mình cần gấp ạ
Giúp mình bài này với mình cần gấp ạ



