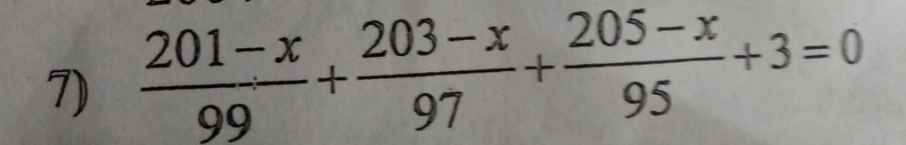\(\dfrac{201-x}{99}+\dfrac{203-x}{97}+\dfrac{205-x}{95}+3=0\)
\(\Leftrightarrow\left(\dfrac{201-x}{99}+1\right)+\left(\dfrac{203-x}{97}+1\right)+\left(\dfrac{205-x}{95}+1\right)=0\)
\(\Leftrightarrow\left(\dfrac{300-x}{99}\right)+\left(\dfrac{300-x}{97}\right)+\left(\dfrac{300-x}{95}\right)=0\)
\(\Leftrightarrow\left(300-x\right)\left(\dfrac{1}{99}+\dfrac{1}{97}+\dfrac{1}{95}\right)=0\)
\(\Leftrightarrow300-x=0\)
\(\Leftrightarrow x=300\)
Vậy \(S=\left\{300\right\}\)