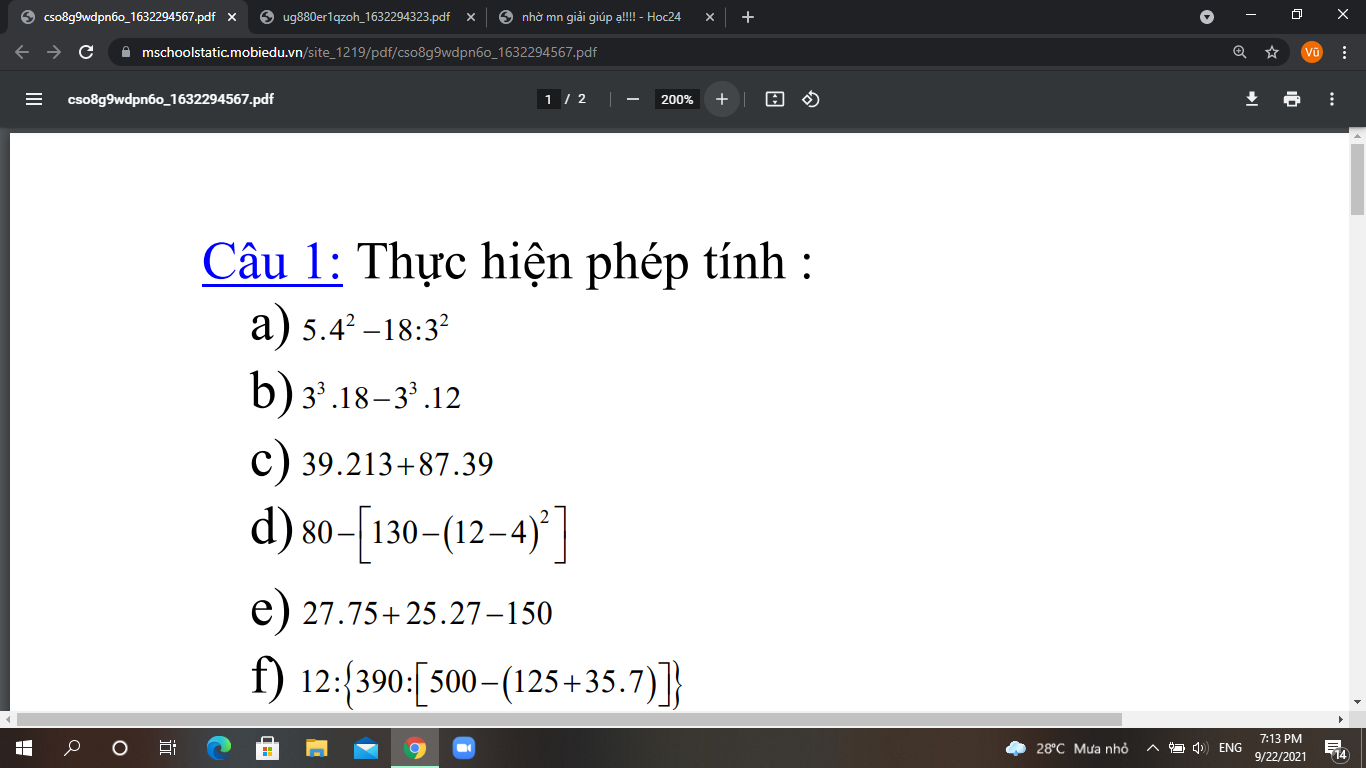
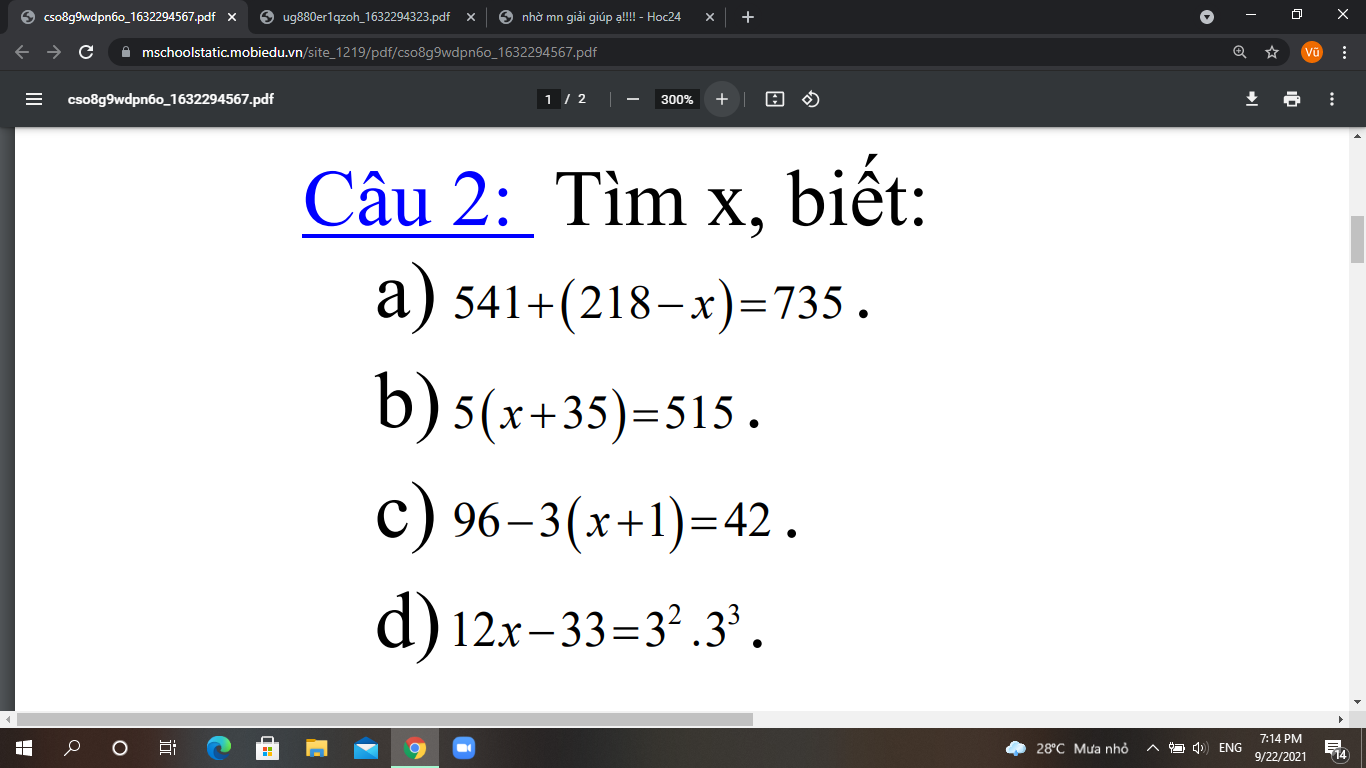
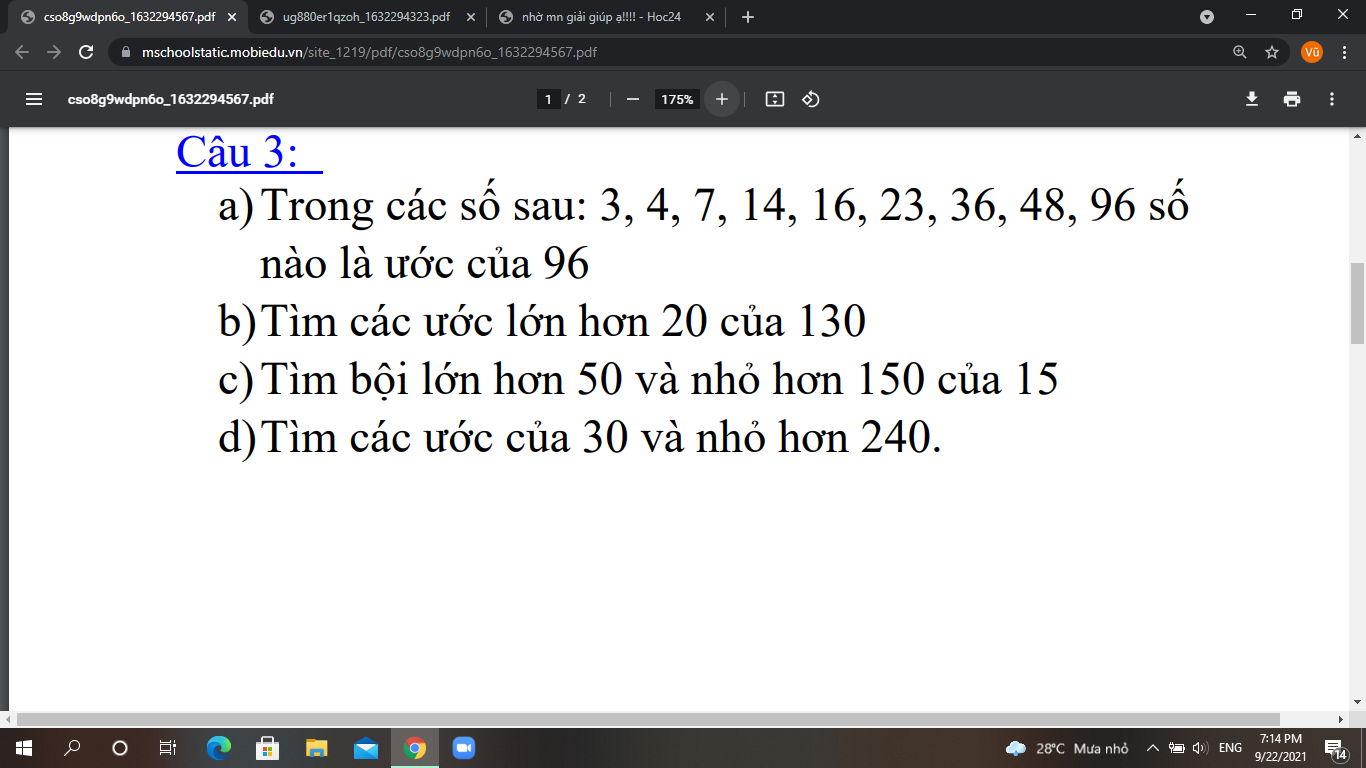
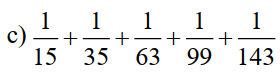a) .
Ta có :
\(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+....+\dfrac{1}{200^2}< \dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+....+\dfrac{1}{199.200}\)
Gọi \(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{199.200}\left(là.B\right)\)
ta có:
\(B=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{199}-\dfrac{1}{200}\)
\(\dfrac{1}{2}-\dfrac{1}{200}< \dfrac{1}{2}\) (1 )
Từ (1) ta suy ra được :
\(A=\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+....+\dfrac{1}{200^2}< \dfrac{1}{2}\left(đ.p.c.m\right)\)
b ) .
Ta có :
\(B=2\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{200^2}\right)\)\(>2\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+....+\dfrac{1}{199.200}\right)\)
gọi vế thứ (2) ở B là C
Ta có :
\(C=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{199}-\dfrac{1}{200}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{200}\right)=\dfrac{99}{100}>\dfrac{9}{20}\) (1)
Từ (1) ta suy ra được :
\(B=\dfrac{2}{2^2}+\dfrac{2}{3^2}+\dfrac{2}{4^2}+.....+\dfrac{2}{200^2}>\dfrac{9}{20}\)








 cần gấp nha giúp mik nha
cần gấp nha giúp mik nha