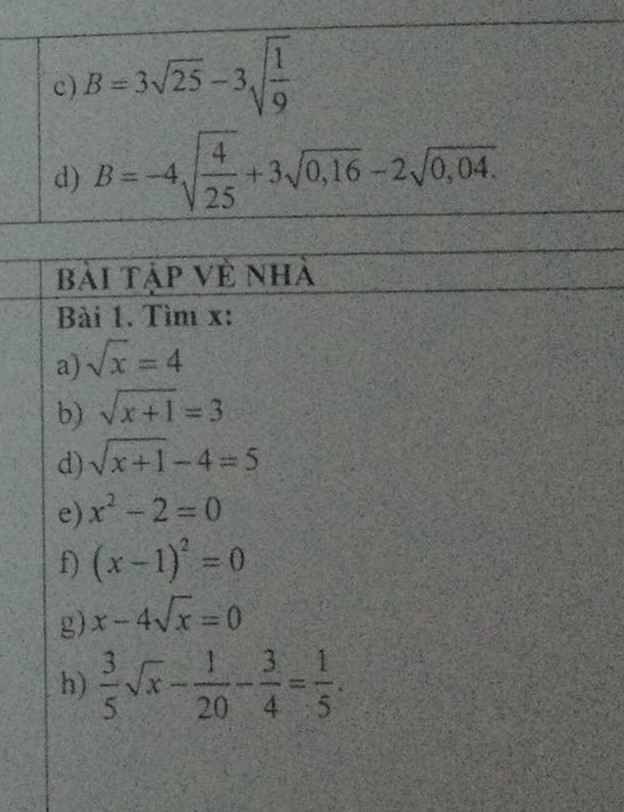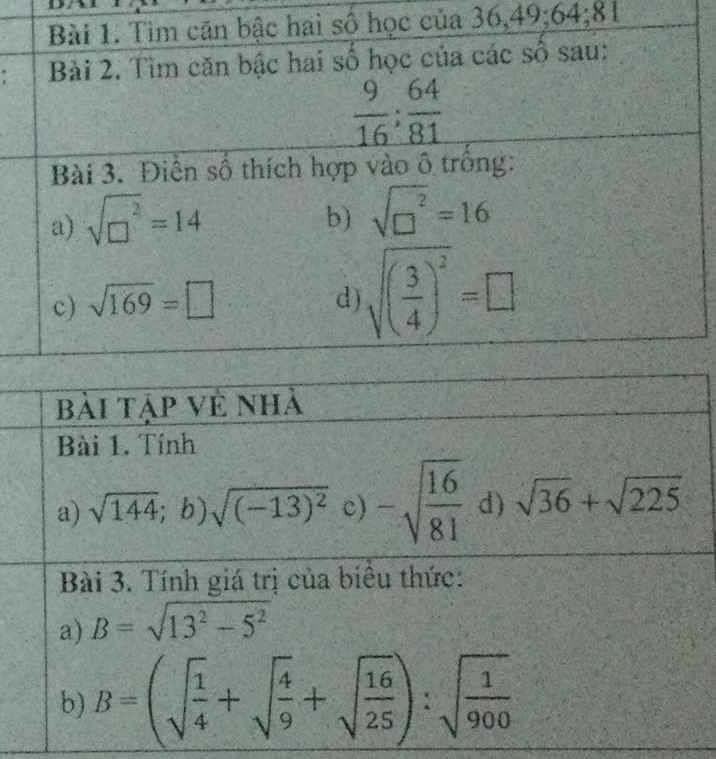Bài 1:
a: \(F\left(x\right)=2x^2-3x+x^3-4+4x-x^3-1\)
\(=\left(x^3-x^3\right)+2x^2-3x+4x-4-1=2x^2+x-5\)
\(G\left(x\right)=3-2x^3+1-x+2x^3+x^2+3x\)
\(=\left(-2x^3+2x^3\right)+x^2+\left(3x-x\right)+\left(1+3\right)=x^2+2x+4\)
b: H(x)=F(x)-G(x)
\(=2x^2+x-5-\left(x^2+2x+4\right)\)
\(=2x^2+x-5-x^2-2x-4=x^2-x-9\)
K(x)=F(x)+G(x)
\(=2x^2+x-5+x^2+2x+4=3x^2+3x-1\)
c: \(H\left(2\right)=2^2-2-9=4-2-9=2-9=-7\)
\(H\left(-2\right)=\left(-2\right)^2-\left(-2\right)-9=4+2-9=6-9=-3\)
Bài 2:
a: \(A\left(x\right)=-x^4-x+5x^2-2x^4-2x+\frac12-4x^2\)
\(=\left(-x^4-2x^4\right)+\left(5x^2-4x^2\right)+\left(-x-2x\right)+\frac12\)
\(=-3x^4+x^2-3x+\frac12\)
\(B\left(x\right)=6x^2-x^4-2x-1\frac12-3x^3-x-2x^4-7x^2+x^3\)
\(=\left(-x^4-2x^4\right)+\left(-3x^3+x^3\right)+\left(6x^2-7x^2\right)+\left(-2x-x\right)-\frac32\)
\(=-3x^4-2x^3-x^2-3x-\frac32\)
\(C\left(x\right)=-9x^3+2x^2-2x-\frac12-x^4+10x^3-x\)
\(=-x^4+\left(-9x^3+10x^3\right)+2x^2+\left(-2x-x\right)-\frac12\)
\(=-x^4+x^3+2x^2-3x-\frac12\)
b: A(x)+B(x)+C(x)
\(=-3x^4+x^2-3x+\frac12-3x^4-2x^3-x^2-3x-\frac32-x^4+x^3+2x^2-3x-\frac12\)
\(=-7x^4-x^3+2x^2-9x-\frac32\)
c: A(x)-B(x)-C(x)
\(=-3x^4+x^2-3x+\frac12+3x^4+2x^3+x^2+3x+\frac32+x^4-x^3-2x^2+3x+\frac12\)
\(=x^4+x^3+3x+\frac52\)
d: 2A(x)-P(x)=3B(x)
=>P(x)=2A(x)-3B(x)
=>\(P\left(x\right)=2\left(-3x^4+x^2-3x+\frac12\right)-3\left(-3x^4-2x^3-x^2-3x-\frac32\right)\)
\(=-6x^4+2x^2-6x+1+9x^4+6x^3+3x^2+9x+\frac92\)
\(=3x^4+6x^3+5x^2+3x+\frac{11}{2}\)
bậc là 4;
Hệ số cao nhất là 3
Hệ số tự do là 11/2
Bài 3:
a: \(A\left(x\right)=-2+4x^6-2x^2-4-8x^6+x^4-7x^2+3x^4\)
\(=\left(4x^6-8x^6\right)+\left(x^4+3x^4\right)+\left(-2x^2-7x^2\right)+\left(-2-4\right)\)
\(=-4x^6+4x^4-9x^2-6\)
\(B\left(x\right)=-4x^6-5x+2-3x^2+2x^4-6x^2+x+2x^4\)
\(=-4x^6+\left(2x^4+2x^4\right)-3x^2-6x^2+\left(-5x+x\right)+2\)
\(=-4x^6+4x^4-9x^2-4x+2\)
b: \(A\left(x\right)=-4x^6+4x^4-9x^2-6\)
Bậc là 6
Hệ số cao nhất là -4
Hệ số tự do là -6
\(B\left(x\right)=-4x^6+4x^4-9x^2-4x+2\)
bậc là 6
Hệ số cao nhất là -4
Hệ số tự do là 2
c: A(x)+B(x)
\(=-4x^6+4x^4-9x^2-6_{}-4x^6+4x^4-9x^2-4x+2\)
\(=-8x^6+8x^4-18x^2-4x-4\)
A(x)-B(x)
\(=-4x^6+4x^4+9x^2-6+4x^6-4x^4+9x^2+4x-2\)
\(=18x^2+4x-8\)
d: A(x)=B(x)
=>A(x)-B(x)=0
=>\(18x^2+4x-8=0\)
=>\(9x^2+2x-4=0\)
\(\Delta=2^2-4\cdot9\cdot\left(-4\right)=4+4^2\cdot9=4+16\cdot9=144+4=148\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[\begin{array}{l}x=\frac{-2-\sqrt{148}}{2\cdot9}=\frac{-2-2\sqrt{37}}{18}=\frac{-1-\sqrt{37}}{9}\\ x=\frac{-2+\sqrt{148}}{2\cdot9}=\frac{-2+2\sqrt{37}}{2\cdot9}=\frac{-1+\sqrt{37}}{9}\end{array}\right.\)
e: M(x)=A(x)-B(x)+x^2
\(=18x^2+4x-8+x^2\)
\(=19x^2+4x-8\)
\(=19\left(x^2+\frac{4}{19}x-\frac{8}{19}\right)\)
\(=19\left(x^2+2\cdot x\cdot\frac{2}{19}+\frac{4}{361}-\frac{156}{361}\right)=19\left(x+\frac{2}{19}\right)^2-\frac{156}{19}\ge-\frac{156}{19}\forall x\)
Dấu '=' xảy ra khi \(x+\frac{2}{19}=0\)
=>\(x=-\frac{2}{19}\)
Bài 4:
a: \(A\left(x\right)=8-x^5+4x-2x^3+x^2-7x^4\)
\(=-x^5-7x^4-2x^3+x^2+4x+8\)
\(B\left(x\right)=x^5-8+3x^2+7x^4+2x^3-3x\)
\(=x^5+7x^4+2x^3+3x^2-3x-8\)
b: P(x)=A(x)+B(x)
\(=-x^5-7x^4-2x^3+x^2+4x+8+x^5+7x^4+2x^3+3x^2-3x-8\)
\(=4x^2+x\)
Q(x)=A(x)-B(x)
\(=-x^5-7x^4-2x^3+x^2+4x+8-x^5-7x^4-2x^3-3x^2+3x+8\)
\(=-2x^5-14x^4-4x^3-2x^2+7x+16\)
c: \(Q\left(-1\right)=-2\cdot\left(-1\right)^5-14\cdot\left(-1\right)^4-4\cdot\left(-1\right)^3-2\cdot\left(-1\right)^2+7\cdot\left(-1\right)+16\)
=2-14+4-2-7+16
=-1
d: P(x)=0
=>\(4x^2+x=0\)
=>x(4x+1)=0
=>\(\left[\begin{array}{l}x=0\\ 4x+1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\\ x=-\frac14\end{array}\right.\)
giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ
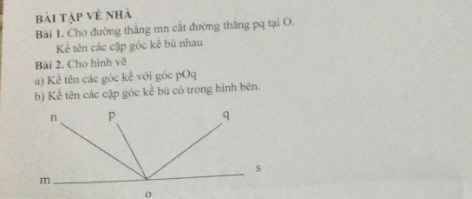
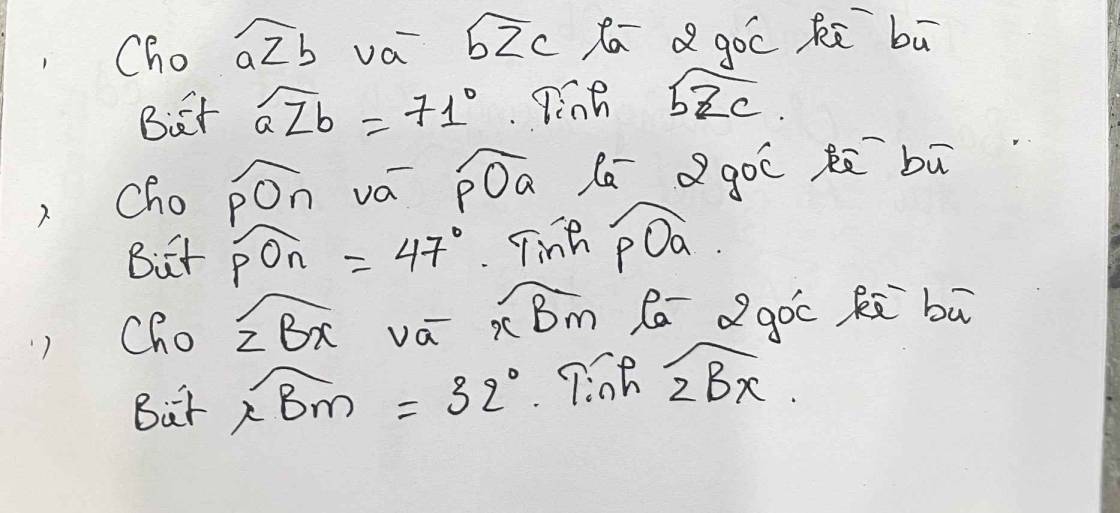GIẢI GẤP GIÚP T Ạ, T CẦN GẤP 
