Question

Cần bài `4;5` 😪

Answer 1

Gg nha bn

 

Answer 2

Tải quan đa là bt hết

Answer 3

4. 

a, b em tự giải

c.

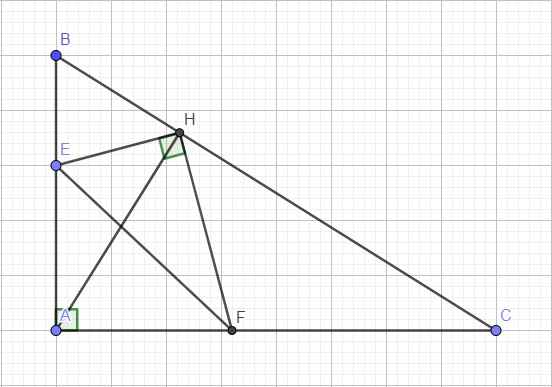
Xét hai tam giác AEH và CFH có:

\(\left\{{}\begin{matrix}\widehat{AHE}=\widehat{CHF}\left(\text{cùng phụ }\widehat{AHF}\right)\\\widehat{EAH}=\widehat{FCH}\left(\text{cùng phụ }\widehat{ABC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta AEH\sim\Delta CFH\left(g.g\right)\)

\(\Rightarrow\dfrac{AE}{CF}=\dfrac{AH}{CH}\Rightarrow AE.CH=AH.CF\)

d. Do \(\Delta AEH\sim\Delta CFH\Rightarrow\dfrac{EH}{FH}=\dfrac{AH}{CH}\Rightarrow\dfrac{EH}{AH}=\dfrac{FH}{CH}\)

\(\Rightarrow FH=\dfrac{EH.CH}{AH}\)

\(\Rightarrow S_{EHF}=\dfrac{1}{2}EH.FH=\dfrac{EH^2.CH}{2AH}\)

Mà H cố định \(\Rightarrow\dfrac{CH}{2AH}\) cố định \(\Rightarrow S_{EHF-min}\) khi \(EH_{min}\)

\(\Rightarrow E\) là hình chiếu vuông góc của H lên AB

Answer 4

Answer 5

5.

Với mọi x;y;z ta có:

\(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)

\(\Leftrightarrow2x^2+2y^2+2z^2\ge2xy+2yz+2zx\)

\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2\)

\(\Leftrightarrow x^2+y^2+z^2\ge\dfrac{1}{3}\left(x+y+z\right)^2\)

Áp dụng:

Đặt vế trái BĐT cần chứng minh là P, ta có:

\(P=\left(a+\dfrac{1}{a}\right)^2+\left(b+\dfrac{1}{b}\right)^2+\left(c+\dfrac{1}{c}\right)^2\)

\(P\ge\dfrac{1}{3}\left(a+\dfrac{1}{a}+b+\dfrac{1}{b}+c+\dfrac{1}{c}\right)^2\)

\(P\ge\dfrac{1}{3}\left(a+b+c+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\ge\dfrac{1}{3}\left(a+b+c+\dfrac{9}{a+b+c}\right)^2\)

\(P\ge\dfrac{1}{3}\left(1+\dfrac{9}{1}\right)^2=\dfrac{100}{3}>33\)