1.
\(sin2x-\sqrt{3}cos2x=2\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow2x=\dfrac{5\pi}{6}+k2\pi\)
\(\Leftrightarrow x=\dfrac{5\pi}{12}+k\pi\)
2.
\(\overrightarrow{AB}=\left(1;-3\right)\)
Đường tròn (C) có tâm \(I\left(1;-2\right)\) và bán kính \(R=3\)
\(T_{\overrightarrow{AB}}\left(C\right)=\left(C'\right)\Rightarrow\left(C'\right)\) có tâm \(I'\left(x';y'\right)\) là ảnh của I qua phép tịnh tiến \(\overrightarrow{AB}\) và bán kính \(R'=R=3\)
\(T_{\overrightarrow{AB}}\left(I\right)=I'\left(x';y'\right)\Rightarrow\left\{{}\begin{matrix}x'=1+1=2\\y'=-3+\left(-2\right)=-5\end{matrix}\right.\)
\(\Rightarrow I'\left(1;-5\right)\)
Phương trình (C'):
\(\left(x-1\right)^2+\left(y+5\right)^2=9\)
3.
Chọn 2 vị trí (trong 7 vị trí) cho số 1: có \(C_7^2\) cách chọn
Còn lại 5 vị trí, chọn 3 vị trí cho chữ số 2: có \(C_5^3\) cách chọn
Còn lại 2 vị trí, chọn 2 chữ số từ 3 chữ số {3;4;5} và xếp thứ tự cho chúng: có \(A_3^2\) cách
Tổng cộng: có \(C_7^2.C_5^3.A_3^2=1260\) số thỏa mãn yêu cầu
4.
Gọi số 4 chữ số cần lập có dạng \(\overline{abcd}\)
TH1: lập số chẵn bất kì:
- Với \(d=0\Rightarrow\) bộ abc có \(A_6^3\) cách
- Với \(d\ne0\Rightarrow d\) có 3 cách chọn (từ 2,4,6), a có 5 cách chọn (khác 0 và d), b có 5 cách chọn (khác a và d), c có 4 cách chọn (khác a,b,d)
\(\Rightarrow A_6^3+3.5.5.4=420\) số
TH2: lập số chẵn có 4 chữ số sao cho ko có mặt chữ số 2, nghĩa là ta lập từ bộ 6 chữ số \(\left\{0;1;3;4;5;6\right\}\)
- Với \(d=0\Rightarrow\) bộ abc có \(A_5^3\) cách
- Với \(d\ne0\Rightarrow d\) có 2 cách chọn (4 hoặc 6), a có 4 cách chọn (khác 0 và d), b có 4 cách chọn (khác a và d), c có 3 cách chọn (khác a,b,d)
\(\Rightarrow A_5^3+2.4.4.3=156\) số
Vậy số số thỏa mãn là: \(420-156=264\) số
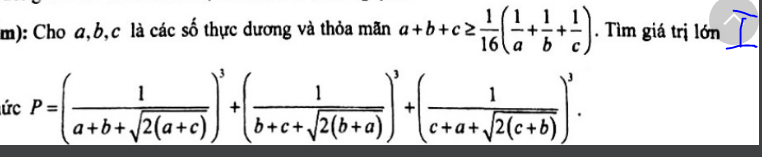mọi người giúp em với em cảm ơn nhiều lắmmmmm
