Các câu hỏi tương tự
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A, B, C, D.a) Tứ giác A, B, C, D là hình gì? Chứng minh rằng .b) Chứng minh rằng điều kiện để tứ giác A, B, C, D là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).c) Chứng minh rằng điều kiện để tứ giác A, B, C, D là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Đọc tiếp
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Trên mặt phẳng (α) cho hình bình hành
A
1
B
1
C
1
D
1
. Về một phía đối với mặt phẳng (α) ta dựng hình bình hành
A
2
B
2
C
2
D
2
. Trên các đoạn
A
1
A...
Đọc tiếp
Trên mặt phẳng (α) cho hình bình hành A 1 B 1 C 1 D 1 . Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A 2 B 2 C 2 D 2 . Trên các đoạn A 1 A 2 , B 1 B 2 , C 1 C 2 , D 1 D 2 ta lần lượt lấy các điểm A, B, C, D sao cho
A A 1 A A 2 = B B 1 B B 2 = C C 1 C C 2 = D D 1 D D 2 = 3
Chứng minh rằng tứ giác ABCD là hình bình hành
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A.D( -8; 5)
B. D( 5; 8)
C.D( 8; 5)
D.D( 8; -5) .
Cho hình chóp S.ABC có SA ⊥ (ABC) và AB ⊥ BC. Số các mặt của tứ diện S.ABC là tam giác vuông là:
A. 1
B. 3
C. 4
D. 2
Cho tứ diện ABCD có tam giác ABC là tam giác cân với BAC
120
o
,ABACa Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là
V
a
3
16
Đọc tiếp
Cho tứ diện ABCD có tam giác ABC là tam giác cân với BAC= 120 o ,AB=AC=a Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16

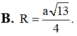
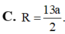
![]()
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho A M A B = A N A C ; gọi I và J lần lượt là trung điểm của BD, CD. Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành? A. AB3CD B. AB2CD C. CD2AB D. CD3AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp ![]() cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?

A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ 4 đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại 4 điểm A’, B’, C’, D’. Tứ giác A’B’C’D’ là hình gì?
A. hình thang
B. hình bình hành
C. hình chữ nhật
D. hình vuông
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)tại H. Chứng minh rằnga) OA⊥BC,OB⊥AC,OC⊥ABb) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BCc) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giácABC.d)Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minhrằng các mặt bên của hình chóp là các tam giác vuông.Bài 8. Cho hình chóp SABCD có đáy ABCD là hình t...
Đọc tiếp
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)
tại H. Chứng minh rằng
a) OA⊥BC,OB⊥AC,OC⊥AB
b) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BC
c) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giác
ABC.
d)
Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minh
rằng các mặt bên của hình chóp là các tam giác vuông.
Bài 8. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D với AD=DC=AB/2 . Gọi I là trung điểm của đoạn AB, SA vuông góc với mặt đáy. Chứng minh rằng
a) Tam giác ABC vuông tại C
b) CI⊥SB,DI⊥SC
c)CB⊥(SAC)
và các mặt bên hình chóp là các tam giác vuông
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất A. Tứ diện đều B. Hình chóp tứ giác đều C. Hình lăng trụ tam giác đều D. Hình hộp chữ nhật
Đọc tiếp
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất
A. Tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác đều
D. Hình hộp chữ nhật




