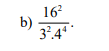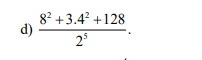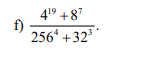Question

Các bn làm nhanh hộ m nhé m cảm ơn <3

Answer 1

b: \(=\dfrac{2^8}{3^2\cdot2^8}=\dfrac{1}{3^2}=\dfrac{1}{9}\)

d: \(=\dfrac{2^6+3\cdot2^4+2^7}{2^5}=\dfrac{2^4\left(2^2+3+2^3\right)}{2^5}=\dfrac{1}{2}\cdot15=\dfrac{15}{2}\)

f: \(=\dfrac{2^{38}+2^{21}}{2^{32}+2^{15}}=\dfrac{2^{21}}{2^{15}}=2^6\)

Answer 2

b) \(\dfrac{16^2}{3^2.4^4}=\dfrac{4^4}{9.4^4}=\dfrac{1}{9}\)

d) \(\dfrac{8^2+3.4^2+128}{2^5}=\dfrac{2^6+3.2^4+2^7}{2^5}=\dfrac{2^4\left(2^2+3+2^3\right)}{2^5}=\dfrac{4+3+8}{2}=\dfrac{15}{2}\)

f) \(\dfrac{4^{19}+8^7}{256^4+32^3}=\dfrac{2^{38}+2^{21}}{2^{32}+2^{15}}=\dfrac{2^{21}\left(2^{17}+1\right)}{2^{15}\left(1+2^{17}\right)}=2^6=64\)