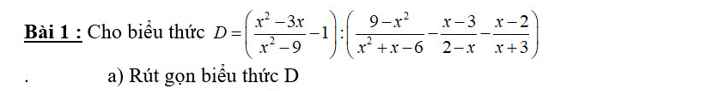a. \(D=\left(\dfrac{x^2-3x}{x^2-9}-1\right):\left(\dfrac{9-x^2}{x^2+x-6}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right)\)
\(=\left[\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-1\right]:\left[\dfrac{\left(3-x\right)\left(3+x\right)}{x^2-2x+3x-6}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\left(\dfrac{x}{x+3}-1\right):\left[\dfrac{\left(3-x\right)\left(3+x\right)}{x\left(x-2\right)+3\left(x-2\right)}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\left(\dfrac{x}{x+3}-\dfrac{x+3}{x+3}\right):\left[\dfrac{\left(3-x\right)\left(3+x\right)}{\left(x-2\right)\left(x+3\right)}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\dfrac{3}{x+3}:\left(\dfrac{3-x}{x-2}-\dfrac{3-x}{x-2}-\dfrac{x-2}{x+3}\right)\)
\(=\dfrac{3}{x+3}:\dfrac{x-2}{x+3}\)
\(=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{3}{x-2}\)