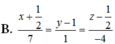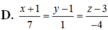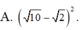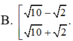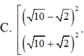C33.4:
Ta có: {x2+y2=1(1)21x+3y+48x2−48y2+28xy=69(2){x2+y2=1(1)21x+3y+48x2−48y2+28xy=69(2)
Từ pt (1) ta có: x2+y2=1⇒y2=1−x2x2+y2=1⇒y2=1−x2
Thay vào pt (2) ta được: 21x+3√1−x2+48x2−48(1−x2)+28x√1−x2−69=021x+31−x2+48x2−48(1−x2)+28x1−x2−69=0
⇔3√(1−x)(1+x)+28x√(1−x)(1+x)−21√(1−x)(1−x)−48(1−x2)−48(1−x2)=0⇔3(1−x)(1+x)+28x(1−x)(1+x)−21(1−x)(1−x)−48(1−x2)−48(1−x2)=0
⇔√1−x(3√1+x+28x√1+x−21√1−x−96(1+x)√1−x)=0⇔1−x(31+x+28x1+x−211−x−96(1+x)1−x)=0
⇔[√1−x=03√1+x+28x√1+x−21√1−x−96(1+x)√1−x=0⇔[1−x=031+x+28x1+x−211−x−96(1+x)1−x=0
+ Nếu √1−x=0⇔1−x=0⇔x=1⇒y=01−x=0⇔1−x=0⇔x=1⇒y=0
+Nếu 3√1+x+28x√1+x−21√1−x−96(1+x)√1−x=031+x+28x1+x−211−x−96(1+x)1−x=0
⇔3√1+x+28x√1+x=21√1−x+96(1+x)√1−x⇔31+x+28x1+x=211−x+96(1+x)1−x
⇔784x3+952x2+177x+9=−9216x3−13248x2+8775x+13689⇔784x3+952x2+177x+9=−9216x3−13248x2+8775x+13689
⇔10000x3+14200x2−8598x−13680=0⇔10000x3+14200x2−8598x−13680=0
⇔x=2425⇒y=725⇔x=2425⇒y=725
Thay x=2424;y=725x=2424;y=725 vào hệ pt ta thấy thoả mãn
x=2425;y=725x=2425;y=725 là 1 cặp nghiệm của hệ pt
Vậy hệ pt có nghiệm: (x;y)∈{(2425;725),(1;0)}(x;y)∈{(2425;725),(1;0)}
Đúng hay sai? ![]()
Đúng nhưng có người trả lời rồi,cop mần chi cho khổ :)