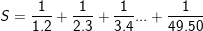Question

 c) 

giúp mình với, giải từng bước một

Answer 1

\(=>S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)

\(S=1-\dfrac{1}{50}=\dfrac{50}{50}-\dfrac{1}{50}=\dfrac{49}{50}\)

Answer 2

\(S=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\)

\(S=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)

\(S=\dfrac{1}{1}-\dfrac{1}{50}\)

\(S=\dfrac{50}{50}-\dfrac{1}{50}\)

\(S=\dfrac{49}{50}\)