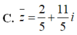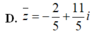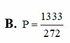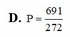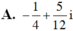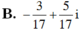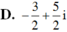\(\dfrac{1-2i}{3+4i}\cdot z=\left(2-i\right)^2\)
=>\(z\cdot\dfrac{\left(1-2i\right)\left(3-4i\right)}{\left(3+4i\right)\left(3-4i\right)}=\left(2-i\right)^2\)
=>\(z\cdot\dfrac{3-4i-6i+8i^2}{9-16i^2}=4-4i+i^2\)
=>\(z\cdot\dfrac{-10i-5}{25}=-4i+3\)
=>\(z=\left(-4i+3\right):\dfrac{-10i-5}{25}=\dfrac{\left(-4i+3\right)\cdot25}{-10i-5}\)
\(\Leftrightarrow z=\dfrac{\left(4i-3\right)\cdot5}{2i+1}=\dfrac{\left(4i-3\right)\left(2i-1\right)\cdot5}{4i^2-1}\)
=>\(z=\dfrac{\left(8i^2-4i-6i+3\right)\cdot5}{-5}=\left(-8-10i+3\right)\cdot\left(-1\right)\)
=>\(z=\left(-10i-5\right)\cdot\left(-1\right)=10i+5\)
=>\(z_1=5-10i\)
\(\Leftrightarrow a=5;b=-10\)
2a+b=2*5-10=0