Chọn C.
Từ giả thiết suy ra 3S = 3 + 2.32 + 3.33 + … + 11.311. Do đó
-2S = S – 3S = 1 + 3 + 32 + … + 310 – 10.311
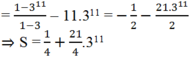
Vì 
![]()
Chọn C.
Từ giả thiết suy ra 3S = 3 + 2.32 + 3.33 + … + 11.311. Do đó
-2S = S – 3S = 1 + 3 + 32 + … + 310 – 10.311
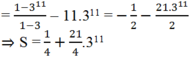
Vì 
![]()
Biết rằng S = 1 + 2.3 + 3.3 2 + ... + 11.3 10 = a + 21.3 b 4 . Tính P = a + b 4 .
A. P =1
B. P =2
C. P =3
D.P = 4
Biết rằng s=1+2.3+\(3.3^2+...+11.3^{10}\)=a+\(\dfrac{21.3^b}{4}\), với a là số hữu tỉ, b là số nguyên. Tính \(P=a+\dfrac{b}{4}\)
1) cho dãy \(\left(u_n\right)\) xác định bởi \(u_n=2.3^n\) giá trị của \(u_{20}\) với mọi số nguyên dương là
A. 2.\(3^{19}\) B.\(2.3^{20}\) C.\(3^{20}\) D.\(2.3^{21}\)
2) cho dãy \(\left(u_n\right)\) xác định bởi \(u_n=3^n\) số hạng \(u_{n+1}\) là
A. \(3^n+1\) B.\(3^n+3\) C.\(3^n.3\) D.\(3\left(n+1\right)\)
3) cho dãy số \(\left(u_n\right)\) với \(u_n=4^n+2^n\) ba số hạng đầu tiên của dãy là
4) cho dãy số \(\left(u_n\right)\) n ϵ N* biết \(u_n=\dfrac{1}{n+1}\) ba số hạng đầu tiên của dãy số đó là
5) cho dãy số có các số hạng đầu tiên là 5,10,15,20,25,.. số hạng tổng quát của dãy số là
Tinh đao hàm của các hàm số
a (m + n/x^2)^4
b y =(3x-2)^11.(1-2x)^21
c y = căn của 2x-1/2x+1
d y = x . căn của x^2 +4
cho a,b,c là 3 cạnh của 1 tam giác có chu vi bằng 4. chứng minh rằng: \(a^2+b^2+c^2+abc< 8\)
cho a,b,c là 3 cạnh của 1 tam giác có chu vi bằng 4. chứng minh rằng \(a^2+b^2+c^2+abc< 8\)
Biết rằng b>0, a+3b=9 và\(x\underrightarrow{lim}0\)\(\frac{\sqrt[3]{ax+1}-\sqrt{1-bx}}{x}=2\). Khẳng định nào dưới đây sai?
A. 1<a<3. B. b>1. C. a2+b2>12 D. b-a<0
có \(ab=\frac{3}{5}\Leftrightarrow a=\frac{3}{5b}\)
có \(bc=\frac{4}{5}\Rightarrow c=\frac{4}{5b}\)
mà \(ac=\frac{4}{5}\Leftrightarrow\frac{3}{5b}.\frac{4}{5b}=\frac{3}{4}\Leftrightarrow\frac{12}{25.b^2}=\frac{3}{4}\Leftrightarrow12.4=3.25.b^2\)
\(\Leftrightarrow\frac{48}{75}=b^2\Leftrightarrow b^2=\frac{16}{25}\Leftrightarrow b=\pm\frac{4}{5}\)
với \(b=\frac{4}{5}\)thì \(a=3:\left(5.\frac{4}{5}\right)=3:4=\frac{3}{4}\)
\(c=4:\left(5.\frac{4}{5}\right)=4:4=1\)
với \(b=-\frac{4}{5}\)thì \(a=3:\left(5.\frac{-4}{5}\right)=3:-4=-\frac{3}{4}\)
\(c=4:\left(5.\frac{-4}{5}\right)=4:-4=-1\)
vậy \(\left(a;b;c\right)\in\left\{\left(\frac{4}{5};\frac{3}{4};1\right);\left(\frac{-4}{5};\frac{-3}{4};-1\right)\right\}\)
Cho các số thực dương a,b,c thỏa mãn a+b+c=3. Chứng minh rằng:
\(\frac{a+1}{1+b^2}+\frac{b+1}{1+c^2}+\frac{c+1}{1+a^2}\ge3\)