Chọn: D
Cách giải:
Xét phương trình hoành độ giao điểm
![]()
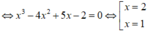
![]()
![]()
Chọn: D
Cách giải:
Xét phương trình hoành độ giao điểm
![]()
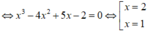
![]()
![]()
Biết rằng đồ thị hàm số y = x 3 - 3 x 2 + 2 x - 1 cắt đồ thị hàm số y = x 2 - 3 x + 1 tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB là:
A. A B = 3
B. A B = 2 2
C. A B = 1
D. A B = 2
Biết rằng đồ thị hàm số y = x 3 - 4 x 2 + 5 x - 1 cắt đồ thị hàm số y=1 tại hai điểm phân biệt A và B. Tính độ dài đoạn bằng AB.
A. AB=2
B. AB=3
C. AB= 2 2
D. AB=1
Biết rằng đồ thị (C) của hàm số y = 2 x + 1 x + 2 luôn cắt đường thẳng d:y=-x+m tại hai điểm phân biệt A và B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Biết rằng đồ thị hàm số y = x + 3 x - 1 và đường thẳng y = x – 2 cắt nhau tại hai điểm phân biệt A(xA;yA) và B(xB;yB). Tính yA + yB.
A. yA + yB = -2
B. yA + yB = 2
C. yA + yB = 4
D. yA + yB = 0
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
Có hai điểm A, B phân biệt thuộc đồ thị hàm số (C): y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đồ thị hàm số y = 4 x - 1 x + 4 cắt đường thẳng y = -x + 4 tại hai điểm phân biệt A, B. Tọa độ điểm C là trung điểm của đoạn thẳng AB là
![]()
![]()
![]()
![]()
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Đồ thị (C) của hàm số cắt đường thẳng Δ: y = -x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB
A. I(-1;1).
B. I(-2;2).
C. I(3;-3).
D. I(6;-6).