Đáp án D
Xét phương trình hoành độ giao điểm
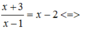
x2 – 4x – 1 = 0
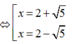
Giả sử A(2 + 5 ; 5 ); B(2 - 5 ; - 5 ) => yA + yB = 0
Đáp án D
Xét phương trình hoành độ giao điểm
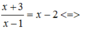
x2 – 4x – 1 = 0
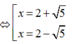
Giả sử A(2 + 5 ; 5 ); B(2 - 5 ; - 5 ) => yA + yB = 0
Biết rằng đường thẳng y = x - 1 cắt đồ thị hàm số y = 2 x - 1 x + 1 tại hai điểm phân biệt A ( x A ; y A ) , B ( x B ; y B ) và x A > x B . Tính giá trị của biểu thức P = y A 2 - 2 y B
A. P = -4
B. P = -1
C. P = 4
D. P = 3
Đường thẳng Δ : y = 2 x + 1 cắt đồ thị (C) của hàm số y = x 3 − x + 3 tại hai điểm A x A ; y A và B x B ; y B , trong đó x A > x B . Tìm x B + y B
A. x B + y B = − 2
B. x B + y B = 4
C. x B + y B = 7
D. x B + y B = − 5
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C). Biết rằng trên (C) có hai điểm A ( x A ; y A ) ; B ( x B ; y B ) phân biệt sao cho các tiếp tuyến với (C) tại A,B có cùng hệ số góc, đồng thời đường thẳng đi qua A và B vuông góc với đường thẳng x+y-5=0. Tính tổng x A + 2 x B + y A + 3 y B , biết x A > x B .
A. 8
B. 2
C. 6
D. 10
Biết A ( x A ; y A ) ; B ( x B ; y B ) là hai điểm thuộc đồ thị (C) của hàm số y = x 3 - 3 x 2 + 2 sao cho tiếp tuyến tại A,B song song và độ dài A B = 4 2 . Giá trị của P = y A + y B - 2 x A x B bằng
![]()

![]()
![]()
Có bao nhiêu cặp điểm A, B thuộc ( C ) : y = 2 x - 1 x - 1 thỏa mãn x A + y A = 5 x B + y B = 5 , ( A ≠ B )
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A, B có tọa độ các điểm A( x A ; y A ; z A ), B( x B ; y B ; z B ). Tọa độ trung điểm M của đoạn thẳng AB là:
A. x A + x B ; y A + y B ; z A + z B
B. x B - x A ; y B - y A ; z B - z A
C. x A + x B 2 ; y A + y B 2 ; z A + z B 2
D. x B - x A 2 ; y B - y A 2 ; z B - z A 2
Cho mặt cầu S : x - 2 2 + y 2 + z + 1 2 = 14 . Mặt cầu (S) cắt trục Oy tại A, B y A < y B . Mặt phẳng tiếp xúc với mặt cầu (S) tại B là.
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A( x A ; y A , z A ), B( x B ; y B , z B ), C( x C ; y C , z C ). Gọi M là trung điểm của BC, G là trọng tâm tam giác ABC. Khẳng định nào sau đây là sai?
A. M x B + x C 2 ; y B + y C 2 ; z B + z C 2
B. AB → = x B - x A ; y B - y A ; z B - z A
C. G x A + x B + x C 3 ; y A + y B + y C 3 ; z A + z B + z C 3
D. AB = ( x B - x A ) 2 ; y B - y A 2 ; ( z B - z A ) 2
Trong không gian Oxyz Cho A(0; 0; a), B(b; 0; 0), C(0; c; 0). Phương trình mặt phẳng (ABC) là:
A. x a + y b + z c = 1 B. x a + y c + z b = 1
C. x b + y c + z a = 1 D. x c + y b + z a = 1