Ta có:
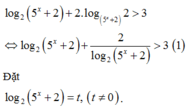
Ta có
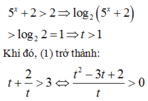
Ta có bảng xét dấu sau:
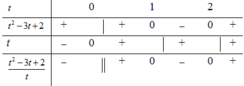
Từ BBT kết hợp điều kiện của t ta có:

Chọn: D
Ta có:
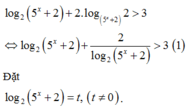
Ta có
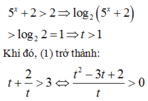
Ta có bảng xét dấu sau:
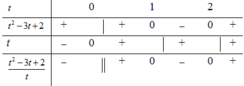
Từ BBT kết hợp điều kiện của t ta có:

Chọn: D
Biết rằng bất phương trình log 2 5 x + 2 + 2 log 5 x + 2 2 > 3 có tập nghiệm là S = log a b ; + ∞ , với a, b là các số nguyên dương nhỏ hơn 6 và a ≠ 1. Tính P = 2 a + 3 b
A. P = 16
B. P = 7
C. P = 11
D. P = 18
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Biết rằng bất phương trình log 2 5 x + 2 + 2 log 5 x + 2 2 > 3 có tập nghiệm là S = log a b ; + ∞ , a, b là các số nguyên dương nhỏ hơn 6 và a ≠ 1 . Tính P = 2 a + 3 b
A. P = 16
B. P = 7
C. P = 11
D. P = 18
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = (a;b)\{x0}. Giá trị của a + b – x0 bằng:
A. 100
B. 30
C. 150
D. 50
Cho log 2 = a , log 3 = b . Biểu diễn log 625 270 theo a và b là:
A. 1 4 3 b + 1 1 - a
B. a + 2 b 2 3 a 1 - b
C. a + b 2 4 a 1 - b
D. a + b 2 2 a 1 - b
Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x - 2 log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Phương trình 5 x 2 - 3 x + 2 = 3 x - 2 có 1 nghiệm dạng x = log a b với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó a+2b bằng
A. 35
B. 30
C. 40
D. 25
Gọi S là tập tất cả các giá trị thực của tham số m để bất phương trình
x 6 + 3 x 4 − m 3 x 3 + 4 x 2 − m x + 2 ≥ 0 có nghiệm với mọi x ∈ ℝ . Biết rằng S = a ; b , a , b ∈ ℝ . Tính P = 2 b − 3 a
A. P = 5
B. P = 10
C. P = 15
D. P = 0