\(f\left(x\right)=\dfrac{x^2-mx+1}{x-m}\)
\(f'\left(x\right)=\dfrac{\left(2x-m\right)\left(x-m\right)-x^2+mx-1}{\left(x-m\right)^2}=\dfrac{x^2-2mx+m^2-1}{\left(x-m\right)^2}\)
\(f'\left(x\right)=0\Rightarrow\left(x-m\right)^2=1\Rightarrow\left[{}\begin{matrix}x=m+1\\x=m-1\end{matrix}\right.\)
bbt:
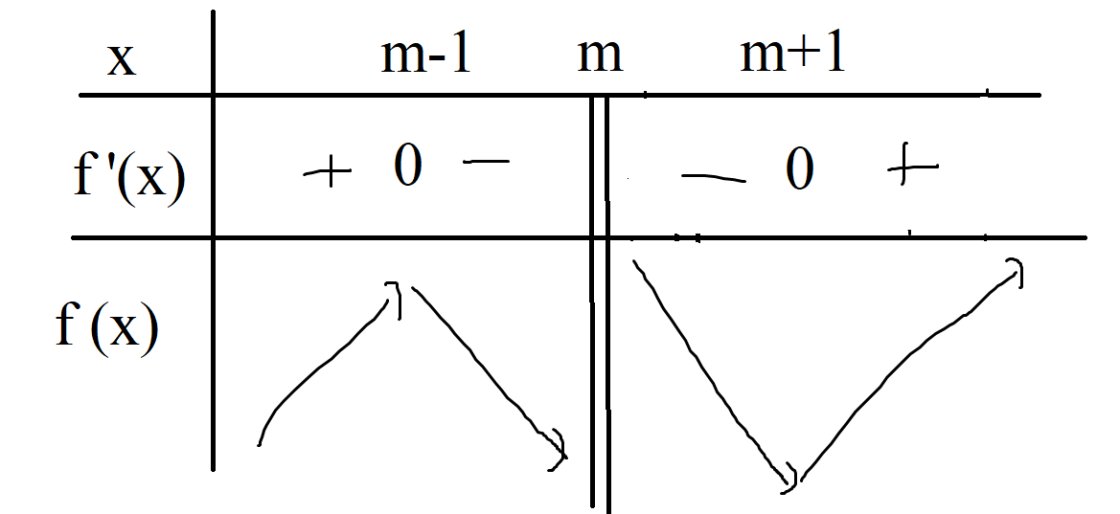
Giá trị lớn nhất của \(f\left(x\right)\) trên \(\left(-\infty,0\right)\) là \(f\left(-1\right)\) thì \(\left\{{}\begin{matrix}m-1=-1\\m\ge0\end{matrix}\right.\)
\(\Rightarrow m=0\Rightarrow f\left(x\right)=\dfrac{x^2+1}{x}\)
bbt:
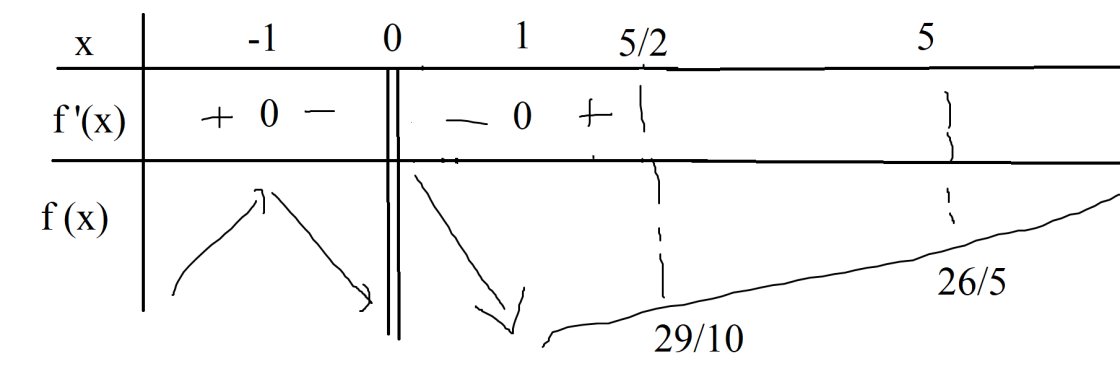
\(\Rightarrow f\left(x\right)_{max\left[\dfrac{5}{2},5\right]}+f\left(x\right)_{min\left[\dfrac{5}{2},5\right]}=f\left(\dfrac{5}{2}\right)+f\left(5\right)=\dfrac{29}{10}+\dfrac{26}{5}=\dfrac{81}{10}\)