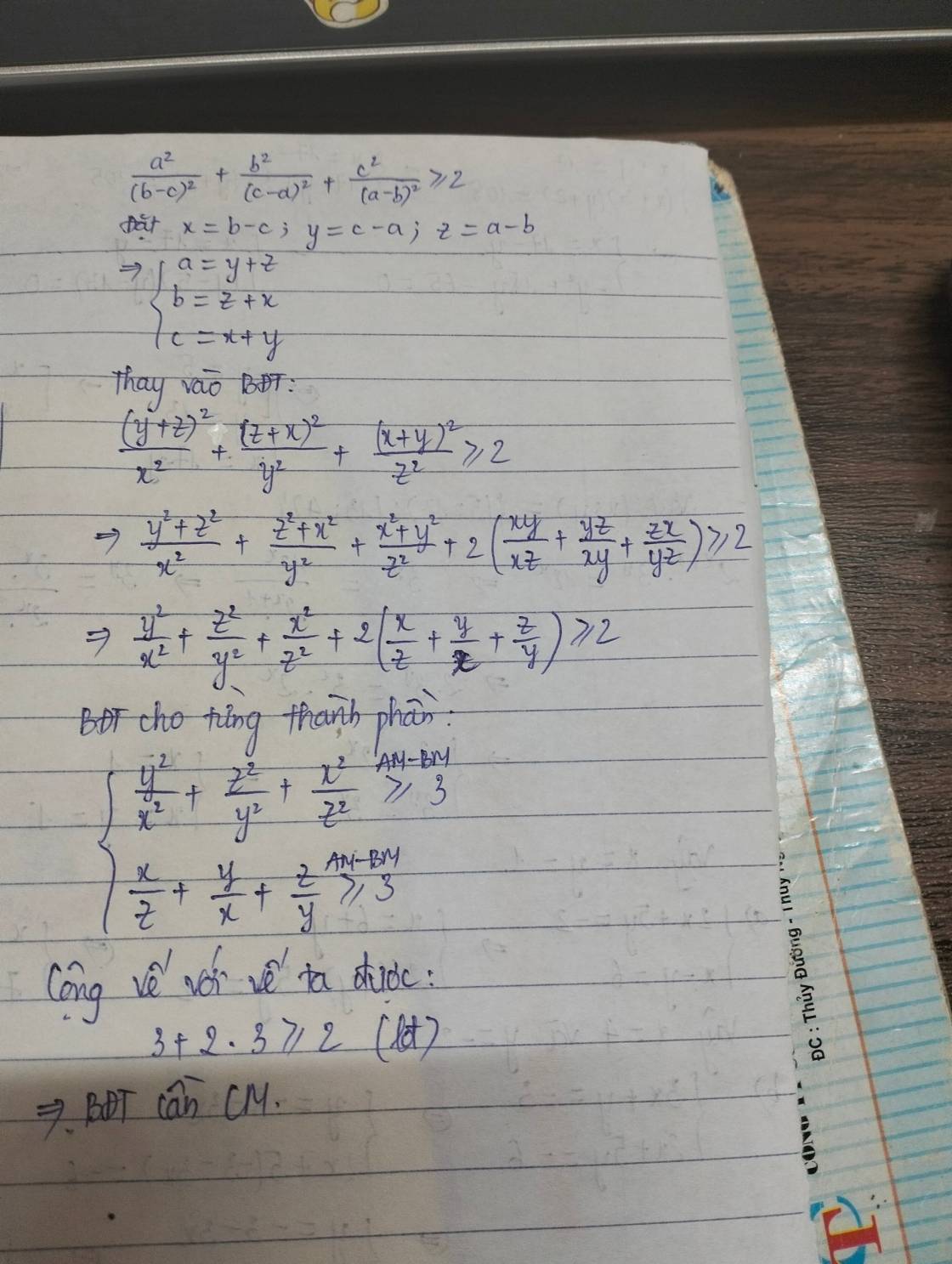Các câu hỏi tương tự
\(1,Cho.a,b,c\ge1.CMR:\left(a-\dfrac{1}{b}\right)\left(b-\dfrac{1}{c}\right)\left(c-\dfrac{1}{a}\right)\ge\left(a-\dfrac{1}{a}\right)\left(b-\dfrac{1}{b}\right)\left(c-\dfrac{1}{c}\right)\)
2, Cho a,b,c>0.CMR:
\(\dfrac{a+b}{bc+a^2}+\dfrac{b+c}{ac+b^2}+\dfrac{c+a}{ab+c^2}\le\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Chứng minh rằng:
\(\left(\dfrac{a+b}{a-b}\right)^2+\left(\dfrac{b+c}{b-c}\right)^2+\left(\dfrac{c+a}{c-a}\right)^2\ge2\)
cho a,b,c>0 tm abc=1. cmr \(\dfrac{1}{a^3\left(b+c\right)}\) + \(\dfrac{1}{b^3\left(c+a\right)}\) +\(\dfrac{1}{c^3\left(a+b\right)}\)≥\(\dfrac{3}{2}\)
Sử dụng BĐT Bunhiacopxki cộng mẫu, lm bài toán sau:
Cho a,b,c là các số thực dương. CMR:
\(\dfrac{2\left(b+c-a\right)^2}{2a^2+\left(b+c\right)^2}+\dfrac{2\left(c+a-b\right)^2}{2b^2+\left(c+a\right)^2}+\dfrac{2\left(a+b-c\right)^2}{2c^2+\left(a+b\right)^2}\ge1\)
Tính:
\(A=\dfrac{a^2}{\left(a-b\right)\left(a-c\right)}+\dfrac{b^2}{\left(b-a\right)\left(b-c\right)}+\dfrac{c^2}{\left(c-a\right)\left(c-b\right)}\)
Cho ba số a, b, c có tổng khác 0 thỏa mãn \(a\left(a^2-bc\right)+b\left(b^2-ac\right)+c\left(c^2-ab\right)=0\). Tính giá trị của biểu thức \(P=\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\)
Cho x,y,z≠0. Tìm GTNN của:
\(T=\dfrac{a^2}{a^2+\left(b+c\right)^2}+\dfrac{b^2}{b^2+\left(a+c\right)^2}+\dfrac{c^2}{c^2+\left(b+c\right)^2}\)
Chứng minh rằng: \(\left(a^2+b^2+c^2\right)\left[\left(\dfrac{1}{\left(a-b\right)^2}+\dfrac{1}{\left(b-c\right)^2}+\dfrac{1}{\left(c-a\right)^2}\right)\right]\ge\dfrac{9}{2}\)