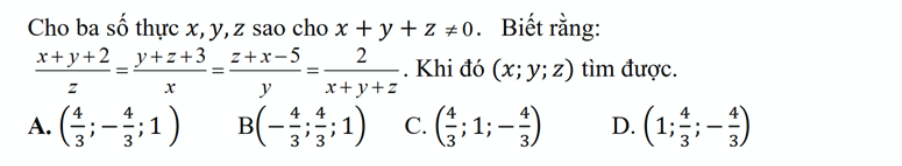\(\dfrac{x+y+2}{z}=\dfrac{y+z+3}{x}=\dfrac{z+x-5}{y}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2=\dfrac{2}{x+y+z}\\ \Rightarrow\left\{{}\begin{matrix}x+y+2=2z\\y+z+3=2x\\z+x-5=2y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y=2z-2\\y+z=2x-3\\z+x=2y+5\end{matrix}\right.\left(1\right)\)
Mà \(\dfrac{2}{x+y+z}=2\Rightarrow x+y+z=1\Rightarrow\left\{{}\begin{matrix}x+y=1-z\\y+z=1-x\\x+z=1-y\end{matrix}\right.\)
Thay vào hệ \(\left(1\right)\Rightarrow\left\{{}\begin{matrix}2z-2=1-z\\2x-3=1-x\\2y+5=1-y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3z=3\\3x=4\\3y=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=-\dfrac{4}{3}\\z=1\end{matrix}\right.\Rightarrow\left(x;y;z\right)=\left(\dfrac{4}{3};-\dfrac{4}{3};1\right)\)
Chọn A