a: \(8t^2-4t=0\)
=>\(4t\left(2t-1\right)=0\)
=>t(2t-1)=0
=>\(\left[{}\begin{matrix}t=0\\2t-1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}t=0\\t=\dfrac{1}{2}\end{matrix}\right.\)
b: \(2t^2-16=0\)
=>\(2t^2=16\)
=>\(t^2=8\)
=>\(t=\pm2\sqrt{2}\)
c: \(5t^2+7t=0\)
=>\(t\left(5t+7\right)=0\)
=>\(\left[{}\begin{matrix}t=0\\5t+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=-\dfrac{7}{5}\end{matrix}\right.\)
e: \(64t^2-8t=0\)
=>\(8\cdot\left(8t^2-t\right)=0\)
=>\(8t^2-t=0\)
=>\(t\left(8t-1\right)=0\)
=>\(\left[{}\begin{matrix}t=0\\8t-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=\dfrac{1}{8}\end{matrix}\right.\)
f: \(18t-9t^2=0\)
=>\(t^2-2t=0\)
=>t(t-2)=0
=>\(\left[{}\begin{matrix}t=0\\t-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=2\end{matrix}\right.\)
g: \(2t^2=t\)
=>\(2t^2-t=0\)
=>t(2t-1)=0
=>\(\left[{}\begin{matrix}t=0\\2t-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=\dfrac{1}{2}\end{matrix}\right.\)
i: \(3t^2=2t\)
=>\(3t^2-2t=0\)
=>t(3t-2)=0
=>\(\left[{}\begin{matrix}t=0\\3t-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=\dfrac{2}{3}\end{matrix}\right.\)
j: \(4t^2=3t\)
=>\(4t^2-3t=0\)
=>t(4t-3)=0
=>\(\left[{}\begin{matrix}t=0\\4t-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=\dfrac{3}{4}\end{matrix}\right.\)
k: \(t^3=t^2\)
=>\(t^2\left(t-1\right)=0\)
=>\(\left[{}\begin{matrix}t^2=0\\t-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=1\end{matrix}\right.\)
m: \(-t^2=4t^3\)
=>\(4t^3+t^2=0\)
=>\(t^2\left(4t+1\right)=0\)
=>\(\left[{}\begin{matrix}t^2=0\\4t+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}t=0\\t=-\dfrac{1}{4}\end{matrix}\right.\)
n: \(-7t^2=14t^3\)
=>\(14t^3+7t^2=0\)
=>\(2t^3+t^2=0\)
=>\(t^2\left(2t+1\right)=0\)
=>\(\left[{}\begin{matrix}t^2=0\\2t+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=-\dfrac{1}{2}\end{matrix}\right.\)
o: \(t^3-8t^2=0\)
=>\(t^2\left(t-8\right)=0\)
=>\(\left[{}\begin{matrix}t^2=0\\t-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=8\end{matrix}\right.\)
`d)-6t+9t^2=0`
`<=>9t^2-6t=0`
`<=>3t(3t-2)=0`
`<=>3t=0` hoặc `3t-2=0`
`<=>t=0` hoặc `t=2/3`
`h)-t=3t^2`
`<=>3t^2+t=0`
`<=>t(3t+1)=0`
`<=>t=0` hoặc `3t+1=0`
`<=>t=0` hoặc `t=-1/3`
`l)2t^3=3t^2`
`<=>2t^3-3t^2=0`
`<=>t^2(2t-3)=0`
`<=>t^2=0` hoặc `2t-3=0`
`<=>t=0` hoặc `t=3/2`
`p)27t^2-54t^3=0`
`<=>54t^3-27t^2=0`
`<=>27t^2(3t-1)=0`
`<=>27t^2=0` hoặc `3t-1=0`
`<=>t=0` hoặc `t=1/3`











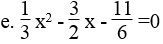 f. 31,1x2 – 50,9x +19,8 =0
f. 31,1x2 – 50,9x +19,8 =0
