đkxđ: \(\dfrac{x+3}{x-1}\ge0\)
Ptr ⇔\(\left(x-1\right)\left(x+3\right)+\dfrac{2\left(x-1\right)\sqrt{\left(x+3\right)\left(x-1\right)}}{x-1}=8\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)+2\sqrt{\left(x-1\right)\left(x+3\right)}-8=0\)
Đặt \(\sqrt{\left(x-1\right)\left(x+3\right)}=a\) (a≥0)
Ptr ⇔ \(a^2+2a-8=0\)
⇔a=2 (tm) hoặc a=-4 (loại)
⇒\(\sqrt{\left(x-1\right)\left(x+3\right)}=2\)
⇔\(x^2+2x-3=4\)
\(\Leftrightarrow x^2+2x-7=0\)
⇔ \(x=-1+2\sqrt{2}\) (tm)
hoặc \(x=-1-2\sqrt{2}\) (tm)
Vậy...

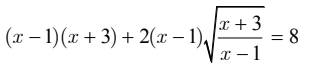 ( bài này giải theo phương pháp đặt ẩn phụ đúng không mọi người ? giải giúp mình với
( bài này giải theo phương pháp đặt ẩn phụ đúng không mọi người ? giải giúp mình với 








