9:
Đặt d=ƯCLN(n+1;n+2)
=>\(\left\{{}\begin{matrix}n+1⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(n+1-n-2⋮d\)
=>\(-1⋮d\)
=>d=1
=>ƯCLN(n+1;n+2)=1
=>\(\dfrac{n+1}{n+2}\) là phân số tối giản
10:
\(A=\dfrac{-1}{20}+\dfrac{-1}{30}+\dfrac{-1}{42}+\dfrac{-1}{56}+\dfrac{-1}{72}+\dfrac{-1}{90}\)
\(=-\left(\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{9\cdot10}\right)\)
\(=-\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=-\left(\dfrac{1}{4}-\dfrac{1}{10}\right)=\dfrac{-3}{20}\)
Bài 11:
ĐKXĐ: n<>-3
Để A là số nguyên thì \(2n⋮n+3\)
=>\(2n+6-6⋮n+3\)
=>\(-6⋮n+3\)
=>\(n+3\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{-2;-4;-1;-5;0;-6;3;-9\right\}\)
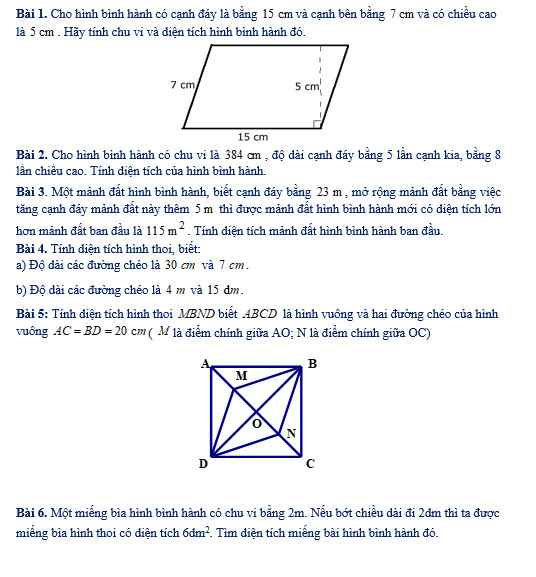làm bài 3 4 5 6 thôi mn nha chậm nhất là 9h30 ạ 
