Các câu hỏi tương tự
Bài 7 (2) :Cho hình thang ABCD (AB//CD) ; hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N . Chứng minh OM = ON
Bài 1: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N. 1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Cho hình thang ABCD (AB//CD), 2 đường chéo cắt nhau tại O. Qua O vẽ đường thẳng sọng song với AB cắt AD và BC lần lượt tại M và N. Chứng minh rằng:
a, OM=ON
b, 1/AB + 1/CD = 2/MN
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
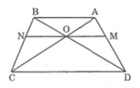
Cho hình thang ABCD (AB//CD).gọi O là giao điểm 2 đường chéo.
a. Chứng minh rằng : OA.OD=OB.OC
b.Kẻ đường thẳng qua O và song song với CD cắt AD,BC lần lượt tại M và N.Chứng minh rằng: ON=OM.
Xem chi tiết
Cho hình thang ABCD (AB // CD), gọi O là giao điểm của hai đường chéo AC và BD.
Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt ở M và N. Chứng minh rằng: OM = ON
cho hình thang ABCD(AB//CD)có 2 đường chéo cắt nhau tại O.
a) CMR: SAOD = SBOC
b) qua O kẻ 1 đường thẳng song song với AB cắt AD, BC lần lượt tại M,N. CMR: OM = ON
Hình thang ABCD ( AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua o và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
a. Chứng minh rằng OM = ON.









