Bài 6 : Cho hình thang cân ABCD ( AB//CD ).Tính các góc của hình tháng cân biết:
a, góc A = 100độ
b,Góc C = 70 độ
c,góc B = góc D
d, góc A = 2.góc C
Bài 9 : Cho tam giác ABC vuông tại A ( AB < AC ).Tia phân giác của góc B cắt AC tại D.Trên BC lấy điểm E sao cho BE = BA. ( bài này vẽ hình giúp e với ạ )
a,Chứng minh tam giác ABD = tam giác EBD
b, Kẻ đường cao AH của tam giác ABC.Chứng minh ADEH là hình thang vuông.
Bài 6
a)
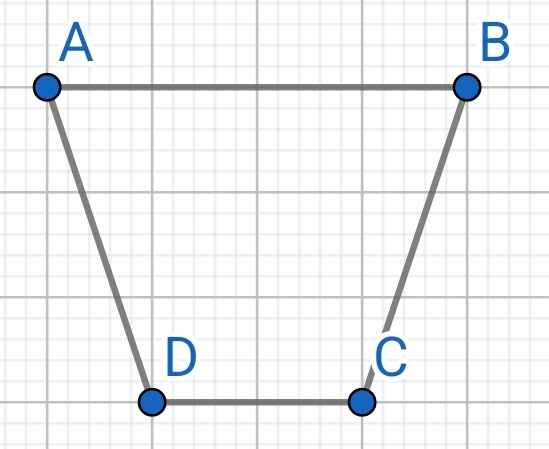
Do ABCD là hình thang cân (gt)
⇒ ∠B = ∠A = 100⁰ và ∠C = ∠D
Ta có:
∠A + ∠B + ∠C + ∠D = 360⁰ (tổng các góc trong hình thang ABCD)
⇒ ∠C + ∠D = 360⁰ - (∠A + ∠B)
⇒ ∠C + ∠D = 360⁰ - (100⁰ + 100⁰)
⇒ ∠C + ∠D = 160⁰
⇒ ∠C = ∠D = 160⁰ : 2 = 80⁰
Bài 6
b)
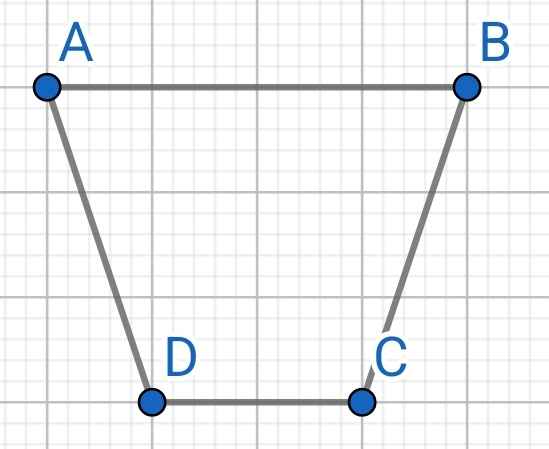
Do ABCD là hình thang cân (gt)
⇒ ∠A = ∠B
Ta có:
∠A + ∠B + ∠C + ∠D = 360⁰ (tổng các góc trong hình thang ABCD)
⇒ ∠A + ∠B = 360⁰ - (∠C + ∠D)
= 360⁰ - (70⁰ + 70⁰)
= 220⁰
⇒ ∠A = ∠B = 220⁰ : 2 = 110⁰
Bài 6
c)
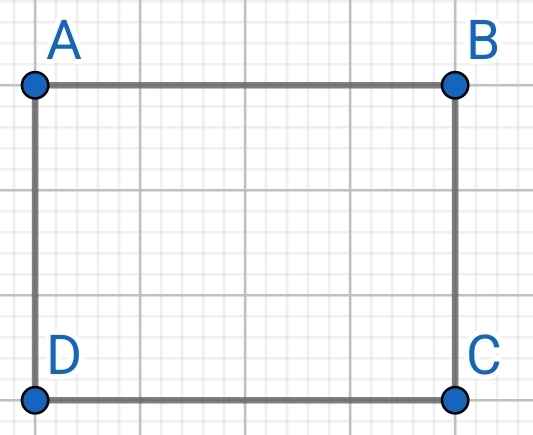
Do ABCD là hình thang cân (gt)
⇒ ∠A = ∠B và ∠C = ∠D
Mà ∠B = ∠D (gt)
⇒ ∠A = ∠B = ∠C = ∠D
Ta có:
∠A + ∠B + ∠C + ∠D = 360⁰ (tổng các góc trong hình thang ABCD)
⇒ ∠A = ∠B = ∠C = ∠D = 360⁰ : 4 = 90⁰
Bài 6
d)
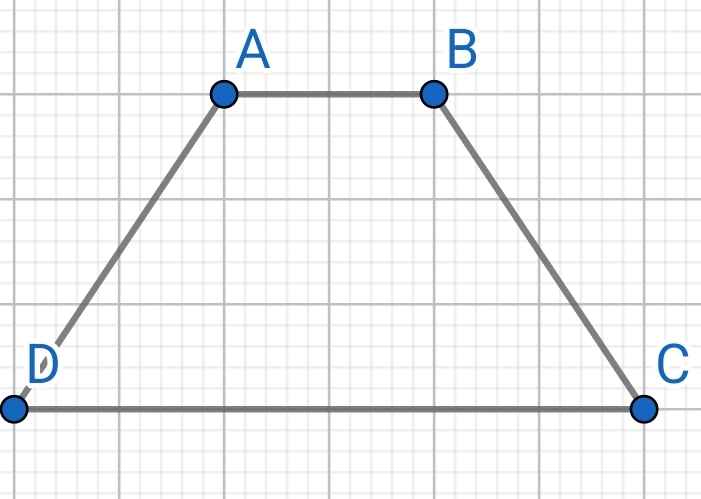
Do ABCD là hình thang cân (gt)
⇒ ∠A = ∠B và ∠C = ∠D
Mà ∠A = 2∠C (gt)
⇒ ∠B = 2∠C
Ta có:
∠A + ∠B + ∠C + ∠D = 360⁰ (tổng các góc trong hình thang ABCD)
⇒ 2∠C + 2∠C + ∠C + ∠C = 360⁰
⇒ 6∠C = 360⁰
⇒ ∠C = 360⁰ : 6 = 60⁰
⇒ ∠A = ∠B = 2.60⁰ = 120⁰
⇒ ∠D = ∠C = 60⁰
Bài 9
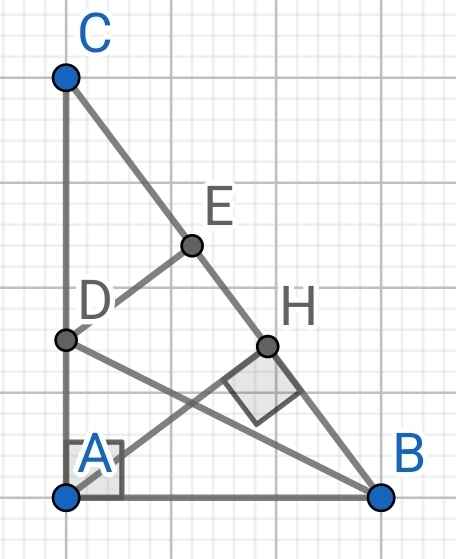
a) Do BD là tia phân giác của ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ BE ⊥ DE
⇒ HE ⊥ DE
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ AH ⊥ HE
Mà HE ⊥ DE (cmt)
⇒ AH // DE
Tứ giác ADEH có:
AH // DE (cmt)
⇒ ADEH là hình thang
Mà AH HE (cmt)
⇒ ADEH là hình thang vuông













