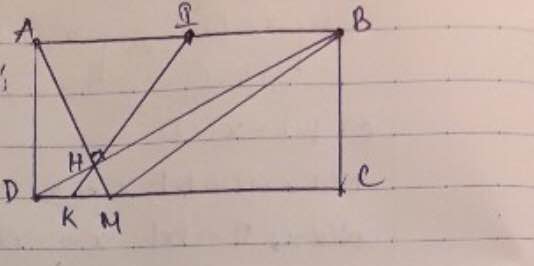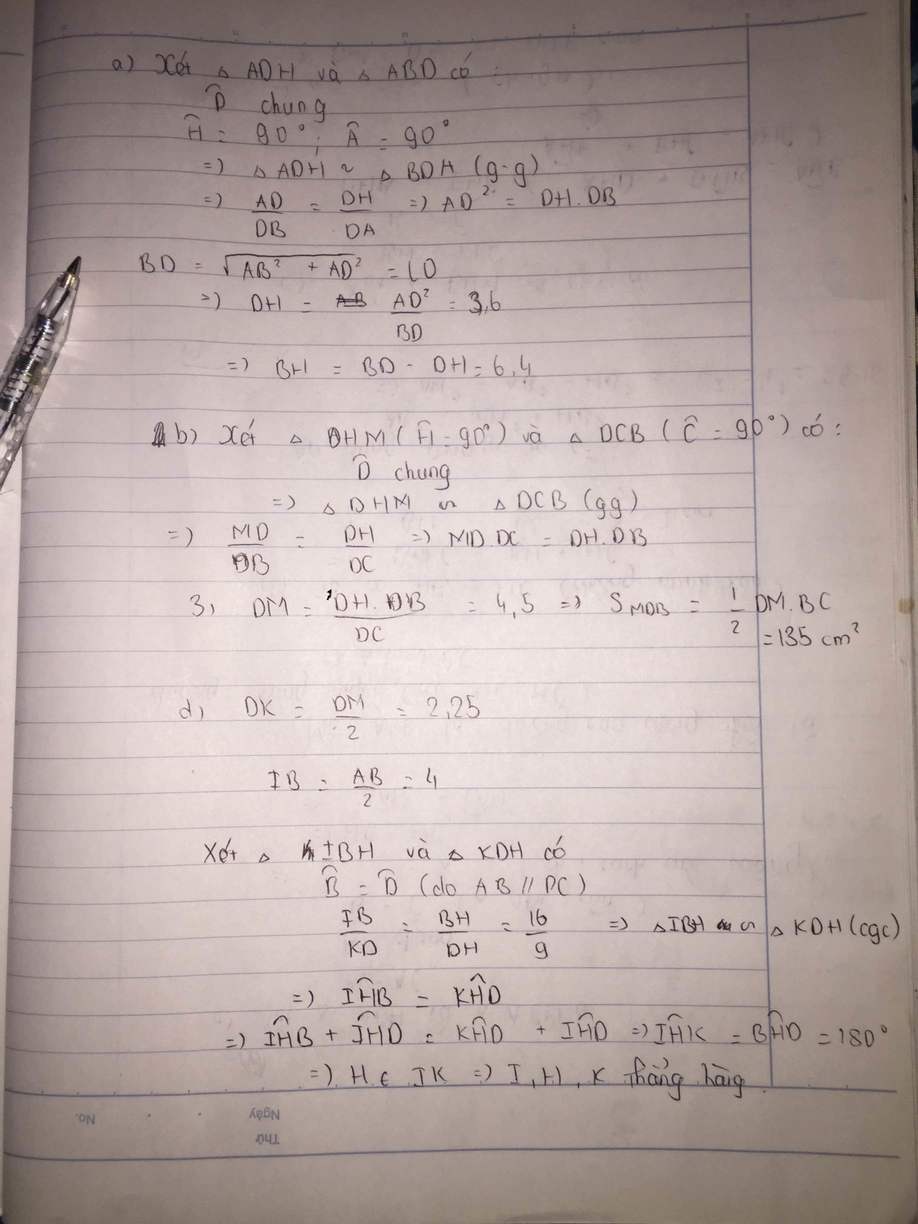Các câu hỏi tương tự
Cho hình chữ nhật ABCD có AD = 6cm , AB = 8cm , hai đường chéo AC và BD cắt nhau tại O . Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại E
a, Kẻ CH vuông góc với DE tại H , gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC và tính tỉ số diện tích của tam giác EHC và diện tích EDB
b, Chứng minh rằng : Ba đường thẳng OE , CD , BH đồng quy
Bài 3 cho tam giác ABC vuông tại A có đường cao AH gọi D, E theo thứ tự là hình chiếu của H trên AB và AC 1) Chứng minh tứ giác ADHE là hình chữ nhật 2) Gọi M và N lần lượt là trung điểm của BH, CHa) Chứng minh DM//ENb) Tính diện tích của tứ giác MDEN nếu diện tích của tam giác ABC là 6cm^23) Gọi O là trung điểm của BC, I là giao của AH và DE vẽ tia Ax vuông góc với tia OI cắt đường thẳng BC tại K chứng minh rằng 3 điểm K, D, E thẳng hàng
Đọc tiếp
Bài 3 cho tam giác ABC vuông tại A có đường cao AH gọi D, E theo thứ tự là hình chiếu của H trên AB và AC
1) Chứng minh tứ giác ADHE là hình chữ nhật
2) Gọi M và N lần lượt là trung điểm của BH, CH
a) Chứng minh DM//EN
b) Tính diện tích của tứ giác MDEN nếu diện tích của tam giác ABC là 6cm^2
3) Gọi O là trung điểm của BC, I là giao của AH và DE vẽ tia Ax vuông góc với tia OI cắt đường thẳng BC tại K chứng minh rằng 3 điểm K, D, E thẳng hàng
Cho hình chữ nhật ABCD có: AB 8cm, BC 6cm, AC cắt BD tại O.Qua B kẻ đường thẳng vuông góc với AC, cắt AC tại H, cắt DC tại M.a/Chứng minh△CMH ∼ △CADb/Chứng minh: BC2 CM.CDc/Tính diện tích tam giác BMCd/Kẻ MK⊥ AB tại K, MK cắt AC tại I.Chứng minh: MI.BMKH.ACe/Chứng minh:góc BIM góc AMCf/ Gọi Q là giao điểm của OE và DC. Chứng minh Q là trung điểm của DCg/Tính tỉ số diện tích △FDC và △EDBh/Chứng minh 3 đường thẳng OE,CD,BF đồng quy.
Đọc tiếp
Cho hình chữ nhật ABCD có: AB= 8cm, BC= 6cm, AC cắt BD tại O.Qua B kẻ đường thẳng vuông góc với AC, cắt AC tại H, cắt DC tại M.
a/Chứng minh△CMH ∼ △CAD
b/Chứng minh: BC2= CM.CD
c/Tính diện tích tam giác BMC
d/Kẻ MK⊥ AB tại K, MK cắt AC tại I.Chứng minh: MI.BM=KH.AC
e/Chứng minh:góc BIM = góc AMC
f/ Gọi Q là giao điểm của OE và DC. Chứng minh Q là trung điểm của DC
g/Tính tỉ số diện tích △FDC và △EDB
h/Chứng minh 3 đường thẳng OE,CD,BF đồng quy.
Cho hình chữ nhật ABCD có AB 8cm; BC 6cm. Kẻ BH vuông góc với AC tại H, DM vuông góc với AC tại M.a) Chứng minh ∆ABH đồng dạng với ∆ACB và suy ra AC.AH AB^2.b) Tính độ dài các đoạn thẳng AC, BH, CH.c) Gọi I là điểm đối xứng với B qua AC. Chứng minh DM IH và ACID là hình thang cân.d) Gọi E, F lần lượt là trung điểm của AH, CD và K là giao điểm của BF với AC. Chứng minh rằng BF.EK ≥ BE.EF.
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 8cm; BC = 6cm. Kẻ BH vuông góc với AC tại H, DM vuông góc với AC tại M.
a) Chứng minh ∆ABH đồng dạng với ∆ACB và suy ra AC.AH = AB^2.
b) Tính độ dài các đoạn thẳng AC, BH, CH.
c) Gọi I là điểm đối xứng với B qua AC. Chứng minh DM = IH và ACID là hình thang cân.
d) Gọi E, F lần lượt là trung điểm của AH, CD và K là giao điểm của BF với AC. Chứng minh rằng BF.EK ≥ BE.EF.
Cho hình chữ nhật ABDC (ABAC) có AH là đường cao của tam giác ABC. Lấy điểm E đối xứng với A qua H. Gọi M và N lần lượt là hình chiếu của BD và CD lên điểm E.Chứng minh ba điểm H, M, N thẳng hàng.Gọi K và P lần lượt là trung điểm của CH và BD. Đường thẳng vuông góc với AK tại K cắt AC tại Q. Chứng minh ba điểm K, Q, P thẳng hàng.Từ trung điểm L của cạnh BD vẽ LI vuông góc với BC tại I. Gọi F đối xứng D qua C. Đường thẳng vuông góc với DF tại F cắt LI tại O. Chứng minh O cách đều B và F.
Đọc tiếp
Cho hình chữ nhật ABDC (AB<AC) có AH là đường cao của tam giác ABC. Lấy điểm E đối xứng với A qua H. Gọi M và N lần lượt là hình chiếu của BD và CD lên điểm E.
Chứng minh ba điểm H, M, N thẳng hàng.Gọi K và P lần lượt là trung điểm của CH và BD. Đường thẳng vuông góc với AK tại K cắt AC tại Q. Chứng minh ba điểm K, Q, P thẳng hàng.Từ trung điểm L của cạnh BD vẽ LI vuông góc với BC tại I. Gọi F đối xứng D qua C. Đường thẳng vuông góc với DF tại F cắt LI tại O. Chứng minh O cách đều B và F.
Cho tam giác ABC vuông tại A. Đường phân giác góc B cắt AC tại D, cho AB= 6cm, BC= 10cm
a) Tính AC, AD, CD
b) Từ D kẻ đường thẳng vuông góc với AC cắt BC tại K. Qua K kẻ đường thẳng vuông góc với BD tại E và cắt AB, AC lần lượt tại F,H. Chứng minh tam giác ABC đồng dạng tam giác DHK
C) Chứng minh BFDK: hình thoi
Cho tam giác ABC có AB 8cm, AC 6cm, BC 10cm. Kẻ đường cao AH( H thuộc BC).a) Chứng minh tam giác ABC vuông tại A. Tính AH, CH.b) Từ H kẻ HE vuông góc với AC( E thuộc AC). Trung tuyến CD ( D thuộc AB) cắt HE, AH lần lượt tại I, K. Chứng minh rằngfrac{KH}{KA}frac{CH}{CB}.c) Chứng minh: I là trung điểm của HE.d) Chứng minh: B, K, E thẳng hàng.
Đọc tiếp
Cho tam giác ABC có AB = 8cm, AC = 6cm, BC = 10cm. Kẻ đường cao AH( H thuộc BC).
a) Chứng minh tam giác ABC vuông tại A. Tính AH, CH.
b) Từ H kẻ HE vuông góc với AC( E thuộc AC). Trung tuyến CD ( D thuộc AB) cắt HE, AH lần lượt tại I, K. Chứng minh rằng\(\frac{KH}{KA}\)=\(\frac{CH}{CB}\).
c) Chứng minh: I là trung điểm của HE.
d) Chứng minh: B, K, E thẳng hàng.
cho hình chữ nhật ABCD có AB=8cm AD=6cm. kẻ đường cao AH của tam giác ABD
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HBA.
b, tính độ dài đoạn thẳng BD, HB.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKH
cho hình chữ nhật ABCD có AB=8cm AD=6cm. kẻ đường cao AH của tam giác ABD
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HBA.
b, tính độ dài đoạn thẳng BD, HB.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKH