1: 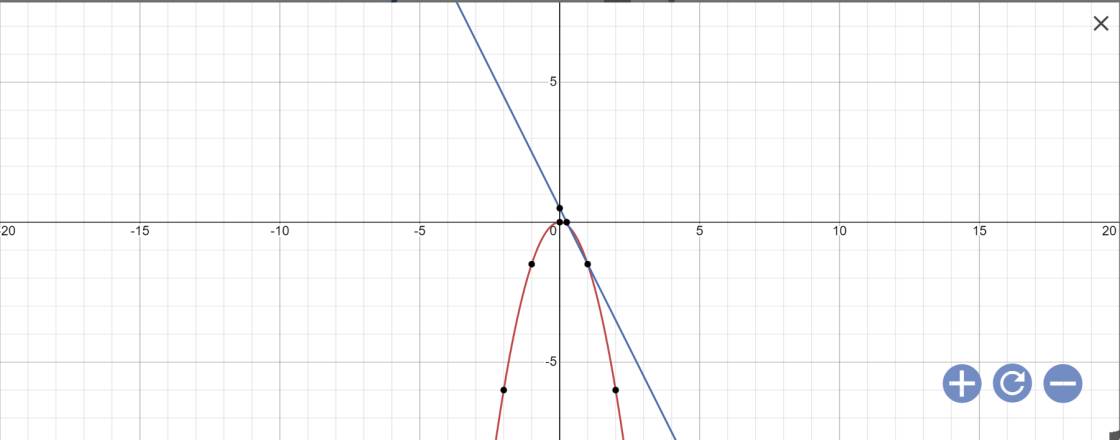
2: Phương trình hoành độ giao điểm là:
\(-\dfrac{3}{2}x^2=-2x+\dfrac{1}{2}\)
=>\(\dfrac{3}{2}x^2-2x+\dfrac{1}{2}=0\)
=>\(3x^2-4x+1=0\)
=>(x-1)(3x-1)=0
=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
Khi x=1 thì \(y=-\dfrac{3}{2}\cdot1^2=-\dfrac{3}{2}\)
Khi x=1/3 thì \(y=-\dfrac{3}{2}\cdot\left(\dfrac{1}{3}\right)^2=-\dfrac{3}{2}\cdot\dfrac{1}{9}=-\dfrac{1}{6}\)
Vậy: (P) giao (d) tại \(A\left(1;-\dfrac{3}{2}\right);B\left(\dfrac{1}{3};-\dfrac{1}{6}\right)\)
a.
\(y=-\dfrac{3}{2}x^2\)
TXĐ: \(D=R\)
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y=-3/2x^2 | -6 | -3/2 | 0 | -3/2 | -6 |
\(y=-2x+\dfrac{1}{2}\)
TXĐ: \(D=R\)
Bảng giá trị:
| x | 0 | 1 |
| y=-2x+1/2 | 1/2 | -3/2 |
Đồ thị:
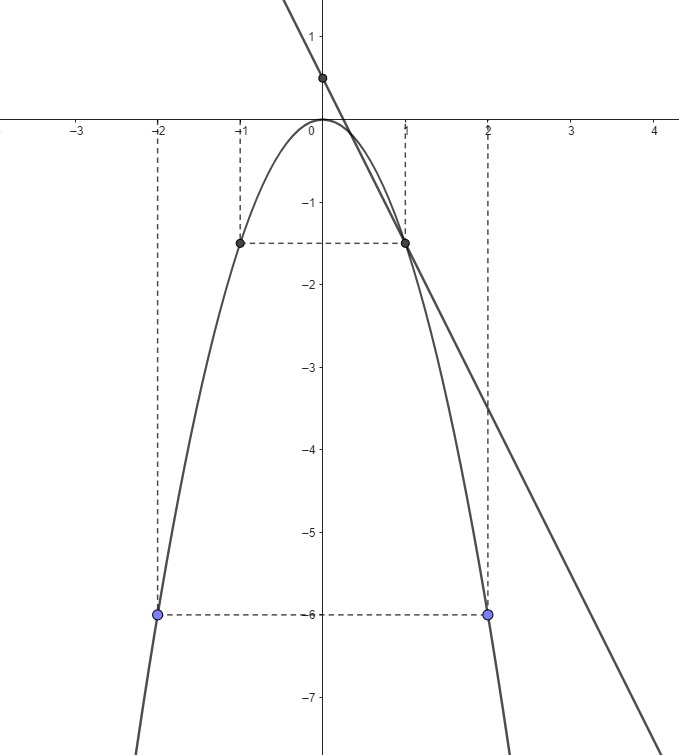
b.
Phương trình hoành độ giao điểm (d) và (P):
\(-\dfrac{3}{2}x^2=-2x+\dfrac{1}{2}\Leftrightarrow3x^2-4x+1=0\)
\(a+b+c=3-4+1=0\Rightarrow\) phương trình có 2 nghiệm:
\(x=1\Rightarrow y=-\dfrac{3}{2}\) và \(x=\dfrac{1}{3}\Rightarrow y=-\dfrac{1}{6}\)
Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(1;-\dfrac{3}{2}\right)\) và \(\left(\dfrac{1}{3};-\dfrac{1}{6}\right)\)














