Bài 3 cho tam giác ABC vuông tại A tia phân giác của góc ABC cắt AC tại k vẽ KI vuông góc với BC với I thuộc BC câu a chứng minh tam giác ABC bằng tam giác ibk từ đó suy ra BK là đường trung trực của ai câu b chứng minh AK nhỏ hơn KC câu c trên tia đối của tia ab lấy điểm E sao cho AE= IC chứng minh ai song song với EC câu D chứng minh tam giác kec cân và BK là đường trung tuyến của tam giác bec Giúp với pls
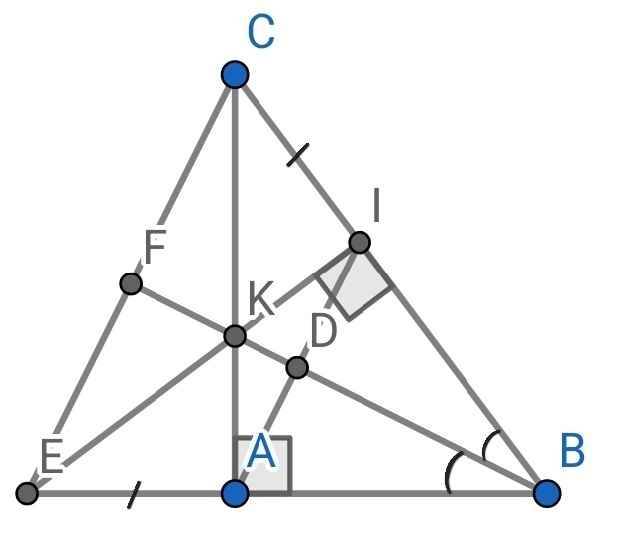
a) Sửa đề: Chứng minh ABK = IBK
Giải
Do BK là tia phân giác của ∠ABC (gt)
⇒ ∠ABK = ∠CBK
⇒ ∠ABK = ∠IBK
Xét hai tam giác vuông: ∆ABK và ∆IBK có:
BK là cạnh chung
∠ABK = ∠IBK (cmt)
⇒ ∆ABK = ∆IBK (cạnh huyền - góc nhọn)
Gọi D là giao điểm của AI và BK
Do ∠ABK = ∠IBK (cmt)
⇒ ∠ABD = ∠IBD
Do ∆ABK = ∆IBK (cmt)
⇒ AB = IB (hai cạnh tương ứng)
Xét ∆ABD và ∆IBD có:
AB = IB (cmt)
∠ABD = ∠IBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆IBD (c-g-c)
⇒ AD = DI (hai cạnh tương ứng)
⇒ D là trung điểm của AI (1)
Do ∆ABD = ∆IBD (cmt)
⇒ ∠ADB = ∠IDB (hai góc tương ứng)
Mà ∠ADB + ∠IDB = 180⁰ (kề bù)
⇒ ∠ADB = ∠IDB = 180⁰ : 2 = 90⁰
⇒ BD ⊥ AI (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AI
⇒ BK là đường trung trực của AI
b) Do ∆ABK = ∆IBK (cmt)
⇒ AK = IK (hai cạnh tương ứng)
∆IKC vuông tại I
KC là cạnh huyền nên là cạnh lớn nhất
⇒ IK < KC
Mà AK = IK (cmt)
⇒ AK < KC
c) Do AB = BI (cmt)
AE = IC (gt)
AB + AE = BI + IC
⇒ BE = BC
⇒ ∆BEC cân tại B
⇒ ∠BEC = ∠BCE = (180⁰ - ∠EBC) : 2 (3)
Do AB = BI (cmt)
⇒ ∆BAI cân tại B
⇒ ∠BAI = ∠BIA = (180⁰ - ∠ABI) : 2
= (180⁰ - ∠EBC) : 2 (4)
Từ (3) và (4) ⇒ ∠BEC = ∠BAI
Mà ∠BEC và ∠BAI là hai góc đồng vị
⇒ AI // EC
d) Do BK là tia phân giác của ∠ABC (gt)
⇒ BK là tia phân giác của ∠EBC
Do ∆BEC cân tại B (cmt)
Mà BK là tia phân giác của ∠EBC (cmt)
⇒ BK cũng là đường trung tuyến của ∆BEC