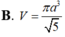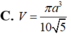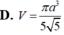Các câu hỏi tương tự
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM A.
V
A
;
−
1
2
.
B.
V
G
;
1
2...
Đọc tiếp
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM
A. V A ; − 1 2 .
B. V G ; 1 2 .
C. V G ; − 2 .
D. V G ; − 1 2 .
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA’, BB’, CC’ sao cho AM2MA, NB2NB, PCPC. Gọi
V
1
,
V
2
lần lượt là thể tích của hai khối đa diện ABCMNP và A’B’C’MNP. Tính tỉ số
V
1
V
2
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA’, BB’, CC’ sao cho AM=2MA', NB'=2NB, PC=PC'. Gọi V 1 , V 2 lần lượt là thể tích của hai khối đa diện ABCMNP và A’B’C’MNP. Tính tỉ số V 1 V 2
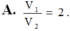
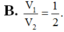
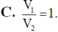
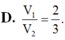
Cho hình lăng trụ đứng có AB a, AC 2a,
A
A
1
2
a
5
và
B
A
C
^
120
0
. Gọi K, I lần lượt là trung điểm của các cạnh
C
C
1
,
B...
Đọc tiếp
Cho hình lăng trụ đứng có AB = a, AC = 2a, A A 1 = 2 a 5 và B A C ^ = 120 0 . Gọi K, I lần lượt là trung điểm của các cạnh C C 1 , B B 1 . Khoảng cách từ điểm I đến mặt phẳng A 1 B K bằng
![]()
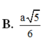

Cho hình lăng trụ đứng
A
B
C
.
A
1
B
1
C
1
có đáy ABC là tam giác vuông tại B, AB 4, BC6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh
B
B
1
,
A
1
B
1
,
B...
Đọc tiếp
Cho hình lăng trụ đứng A B C . A 1 B 1 C 1 có đáy ABC là tam giác vuông tại B, AB= 4, BC=6; chiều cao của lăng trụ bằng 10. Gọi K, M, N lần lượt là trung điểm của các cạnh B B 1 , A 1 B 1 , B C . Thể tích của khối tứ diện C 1 K M N là
A. 15.
B. 5.
C. 45.
D. 10.
Cho hình chóp S.ABC. Gọi M là một điểm thuộc miền trong của tam giác ABC. Từ M kẻ các đường thẳng song song với SA, SB, SC lần lượt cắt các mặt bên SBC, SCA, SAB tại A1, B1, C1. Gọi G1 là trọng tâm tam giác A1B1C1. Tỉ số
S
G
1
S
M
bằng
Đọc tiếp
Cho hình chóp S.ABC. Gọi M là một điểm thuộc miền trong của tam giác ABC. Từ M kẻ các đường thẳng song song với SA, SB, SC lần lượt cắt các mặt bên SBC, SCA, SAB tại A1, B1, C1. Gọi G1 là trọng tâm tam giác A1B1C1. Tỉ số S G 1 S M bằng
![]()
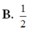
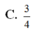
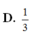
Cho lăng trụ đứng ABC.ABC có diện tích tam giác ABC bằng
2
3
. Gọi M, N, P lần lượt thuộc các cạnh AA, BB, CC, diện tích tam giác MNP bằng 4. Tính góc giữa hai mặt phẳng (ABC) và (MNP).
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có diện tích tam giác ABC bằng 2 3 . Gọi M, N, P lần lượt thuộc các cạnh AA', BB', CC', diện tích tam giác MNP bằng 4. Tính góc giữa hai mặt phẳng (ABC) và (MNP).
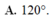
![]()
![]()
![]()
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC. AD3CB3a, ABa, SAa
3
. Điểm I thỏa mãn
A
D
→
3
A
I
→
, M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là...
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC. AD=3CB=3a, AB=a, SA=a 3 . Điểm I thỏa mãn A D → = 3 A I → , M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD)
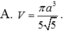
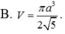
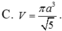
![]()
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho
A
M
+
B
N
+
C
P
1
. Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto
u
→
I
A
→
+
I
B...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ = 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho A M + B N + C P = 1 . Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto u → = I A → + I B → + I C → bằng
![]()
![]()
![]()
![]()
Cho lăng trụ đứng ABC.ABC có diện tích tam giác ABC bằng 5 . Gọi M,N,P lần lượt thuộc các cạnh AA, BB, CC và diện tích tam giác MNP bằng 10. Tính góc giữa hai mặt phẳng (ABC) và (MNP). A.
60
0
B.
30
0
C.
90
0
D.
45
0
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có diện tích tam giác ABC bằng 5 . Gọi M,N,P lần lượt thuộc các cạnh AA', BB', CC' và diện tích tam giác MNP bằng 10. Tính góc giữa hai mặt phẳng (ABC) và (MNP).
A. 60 0
B. 30 0
C. 90 0
D. 45 0
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC;
A
D
3
B
C
3
a
;
A
B
a
;
S
A
a
3
. Điểm I thỏa mãn
A
D
→...
Đọc tiếp
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC; A D = 3 B C = 3 a ; A B = a ; S A = a 3 . Điểm I thỏa mãn A D → = 3 A I → . M là trung điểm SD, H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , SC Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).