a: Xét ΔABC có
M là trung điểm của AB
D là trung điểm của BC
Do đó: MD là đường trung bình của ΔABC
Suy ra: MD//AC
hay AMDC là hình thang
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Bài 2 Cho DABC có AB AC. Gọi M, D lần lượt là trung điểm của các cạnh AB, BC.a) Tứ giác AMDC là hình gì? Vì sao?b) Kẻ đường cao BE cắt MD tại I. Chứng minh I là trung điểm của BEc) Chứng minhBài 2 Cho DABC có AB AC. Gọi M, D lần lượt là trung điểm của các cạnh AB, BC.a) Tứ giác AMDC là hình gì? Vì sao?b) Kẻ đường cao BE cắt MD tại I. Chứng minh I là trung điểm của BEc) Chứng minh goc MBDMED và ED là tia phân giác của góc MEC là tia phân giác của góc MEC
Đọc tiếp
Bài 2 Cho DABC có AB =AC. Gọi M, D lần lượt là trung điểm của các cạnh AB, BC.
a) Tứ giác AMDC là hình gì? Vì sao?
b) Kẻ đường cao BE cắt MD tại I. Chứng minh I là trung điểm của BE
c) Chứng minhBài 2 Cho DABC có AB =AC. Gọi M, D lần lượt là trung điểm của các cạnh AB, BC.
a) Tứ giác AMDC là hình gì? Vì sao?
b) Kẻ đường cao BE cắt MD tại I. Chứng minh I là trung điểm của BE
c) Chứng minh goc MBD=MED và ED là tia phân giác của góc MEC là tia phân giác của góc MEC
Cho tam giác abc có AB=AC . Gọi M,N lần lượt là trung điểm của các cạnh AB,BC
a, Tứ giác AMDC là hình gì
b, Kẻ đường cao BE cắt MD tại I , CM I là trung điểm cảu BE
c,CM góc MBD = góc MED và ED là tia phân giác của góc MEC
Cho DABC vuông tại A, có AB < AC. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh tứ giác DEFB là hình bình hành.
b) Gọi H là điểm đối xứng với F qua AC. Tứ giác AHCF là hình gì? Vì sao?
c) Lấy K là điểm đối xứng với F qua AB. Chứng minh AF, BH, DE, CK đồng quy.
d) Tìm điều kiện của DABC để tứ giác AHCB là hình thang câ
22 tháng 10 2023 lúc 19:51
Cho tam giác ABC có ba góc nhọn (AB<AC), đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh AB,AC,BC.
a) Lấy điểm Q đối xứng với điểm P qua điểm N. Chứng minh tứ giác AQPB là hình bình hành.
b) Tứ giác MNPH là hình gì? Vì sao?
17 tháng 12 2023 lúc 9:31
Cho tam giác ABC vuông tại A, có AB<AC. Gọi M và N lần lượt là trung điểm của AB và AC. Trên tia đối của tia NM lấy điểm D sao cho ND=NM
a. Chứng minh tứ giác BMCD là hình bình hành
b. Tứ giác AMDC là hình gì? Vì sao?
Bài 1: Cho tứ giác ABCD có BC AD và BC không song song với AD, gọi M, N,P, Q, E, F lần lượt là trung điểm của các đoạn thẳng AB, BC, CD, DA, AC, BD.a) Chứng minh tứ giác MEPF là hình thoi.b) Chứng minh các đoạn thẳng MP, NQ, EF cùng cắt nhau tại một điểm.c) Tìm thêm điều kiện của tứ giác ABCD để N, E, F, Q thẳng hàngBài 2: Cho tam giác ABC vuông tại A (AB<AC), M là trung điểm BC, từ M kẻđường thẳng song song với AC, AB lần lượt cắt AB tạt E, cắt AC tại Fa) Chứng minh EFCB là hình thangb) Chứ...
Đọc tiếp
Bài 1: Cho tứ giác ABCD có BC = AD và BC không song song với AD, gọi M, N,
P, Q, E, F lần lượt là trung điểm của các đoạn thẳng AB, BC, CD, DA, AC, BD.
a) Chứng minh tứ giác MEPF là hình thoi.
b) Chứng minh các đoạn thẳng MP, NQ, EF cùng cắt nhau tại một điểm.
c) Tìm thêm điều kiện của tứ giác ABCD để N, E, F, Q thẳng hàng
Bài 2: Cho tam giác ABC vuông tại A (AB<AC), M là trung điểm BC, từ M kẻ
đường thẳng song song với AC, AB lần lượt cắt AB tạt E, cắt AC tại F
a) Chứng minh EFCB là hình thang
b) Chứng minh AEMF là hình chữ nhật
c) Gọi O là trung điểm AM. Chứng minh: E và F đối xứng qua O.
d) Gọi D là trung điểm MC. Chứng minh: OMDF là hình thoi
Bài 3: Cho tam giác ABC có AB<AC. Gọi M, N, P lần lượt là trung điểm của AB,
AC, BC. Vẽ đường cao AH của tam giác ABC. Tứ giác HMNP là hình gì.
Bài 4: Cho tứ giác ABCD có góc DAB = góc BCD = 120 0 . Tính số đo của hai góc
còn lại để ABCD là hình bình hành.
Bài 5: Cho hình bình hành ABCD. Trên đưởng chéo AC chọn hai điểm E và F sao
cho AE=EF=FC.
a) Tứ giác BEDF là hình gì?
b) Chứng minh CFDAEB .
c) Chứng minh CFBEAD .
Bài 6: Cho tam giác ABC cân tại A, đường cao AD. Gọi E là điểm đối xứng với D qua
trung điểm M của AC.
a) Tứ giác ADCE là hình gì? Vì sao?
b) Tứ giác ABDM là hình gì? Vì sao?
c) Tam giác ABC có thêm điều kiện gì thì ADCE là hình vuông?
d) Tam giác ABC có thêm điều kiện gì thì ABDM là hình thang cân?
Bài 4:Cho A4BC . Gọi M là trung điểm cạnh BC và N là trung điểm cạnh
AC. Trên tia MN lấy điểm D sao cho N là trung điểm của MD.
c. Đường thăng BN cắt AM tại E và cắt CD tại F. Chứng minh: BE = EF
b. A.BC có điều kiện gì thì tứ giác AMCD là hình chữ nhật? Vì sao?
a. Chúng minh các tứ giác: AMCD, ABMD là hình bình hành
Xem chi tiết
25 tháng 8 2023 lúc 13:19
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE. a) Tứ giác ADME là hình gì? Vì sao? b) Chứng minh ba điểm A, I, M thẳng hàng. c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DPDM, EQEM Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
Đọc tiếp
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE.
a) Tứ giác ADME là hình gì? Vì sao?
b) Chứng minh ba điểm A, I, M thẳng hàng.
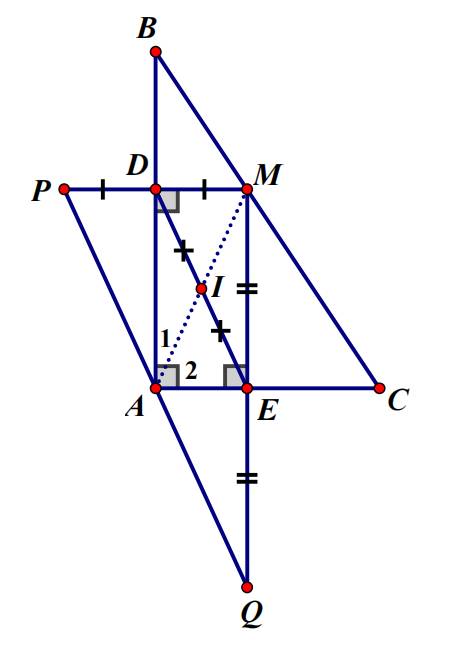
c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DP=DM, EQ=EM
Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
Cho ∆ABC nhọn. Gọi D, E, F lần lượt là trung điểm của các cạnh AC, AB, BC.
a) Tứ giác BEDF là hình gì ? Vì sao ?
b) Gọi H là trực tâm của ∆ABC. Gọi M, N, P lần lượt là trung điểm của HB, HC, HẠ. Chứng minh rằng tứ giác DEMN là hình chữ nhật.
c) Gọi O là giao điểm của MD và EN . Chứng minh rằng ba điểm O, P, F thẳng hàng.