Question

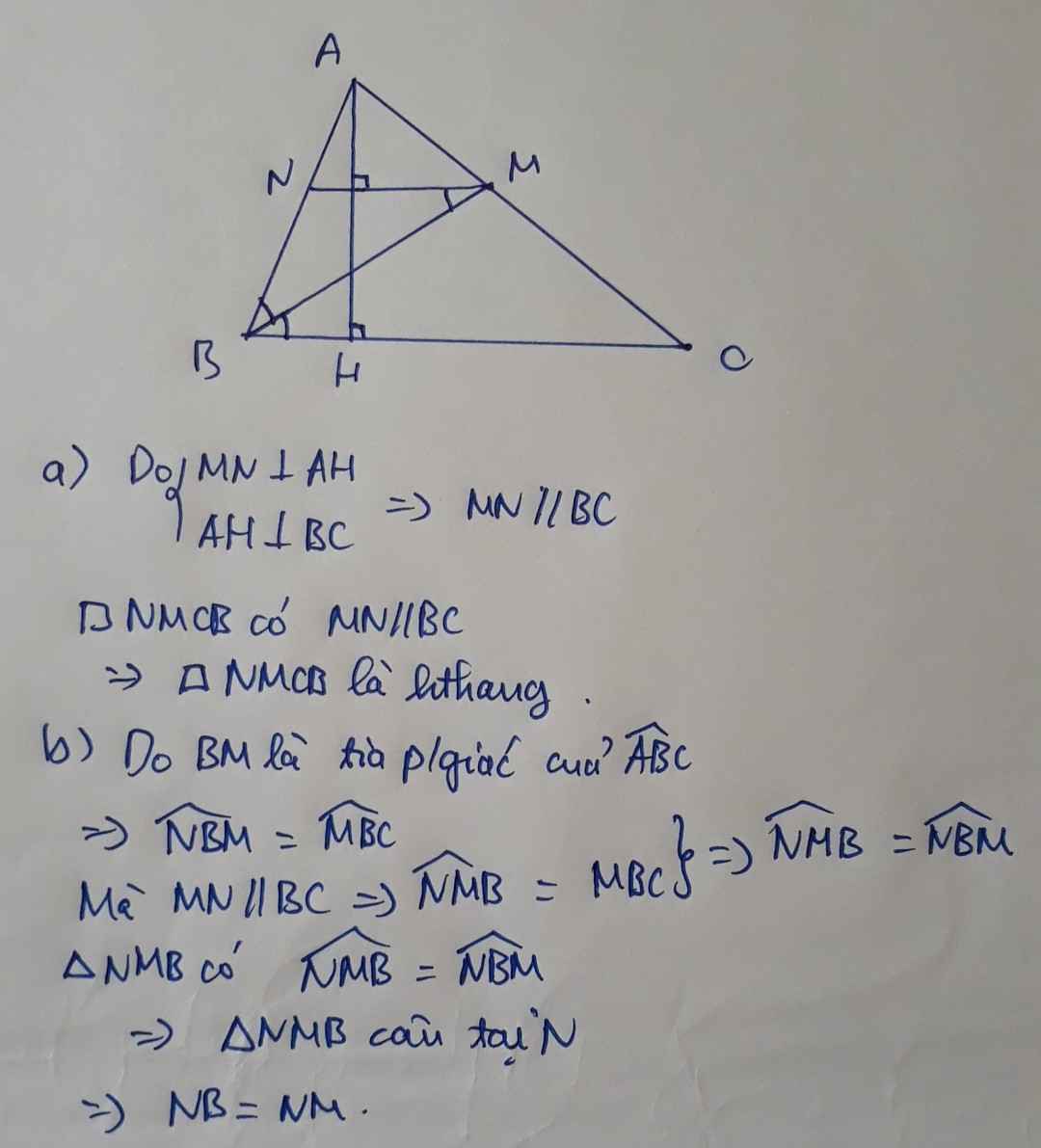
Bài 10 :( bài này vẽ hình giúp e vs ạ ) Cho tam giác nhọn ABC có AH là đường cao.Tia phân giác của góc B cắt AC tại M.Từ M kẻ đường thẳng vuông góc AH , đường thẳng này cắt AB ở N.Chứng Minh rằng ;

a, MN//BC,từ đó suy ra tứ giác BCMN là hình thang

b, góc NMB = góc NBM , từ đó suy ra BN = MN

Bài 13 : Cho hình thang cân ABCD có AB // CD và AB < CD , hai đường cao AH,BK (hình vẽ) .Chứng minh : a, Tam giác AHD = tam giác BEC ; b, AB = HK ; c, KC =\(\dfrac{DC-AB}{2}\)

Bài 18 :Cho hình thang ABCD như hình vẽ.Biết AC = BD.

a, Chứng minh hình thang ABCD là hình           

thang cân.

b,Chứng minh tam giác ABD = tam giác DCA

c, Chứng minh góc ADB = góc DAC

Answer 1

Answer 2

Bài 18: 

a) Tứ giác `ABCD` là hình thang có: `AC = BD`

=> Tứ giác `ABCD` là hình thang cân

b) Do tứ giác `ABCD` là hình thang cân

`=> {(AB = CD),(hat{BAD} = hat{CDA}):}`

Xét `ΔABD` và `ΔDCA` có: 

`AB = CD` (chứng minh trên)

`hat{BAD} = hat{CDA}` (chứng minh trên)

`AD` chung

`=>  ΔABD= ΔDCA` (cạnh góc cạnh)

c) Từ câu `b,  ΔABD= ΔDCA`

`=> hat{BDA} = hat{CAD} `

Answer 3