Bài 1: Tính diện tích mặt cầu và thể tích hình cầu có bán kính là 2cm
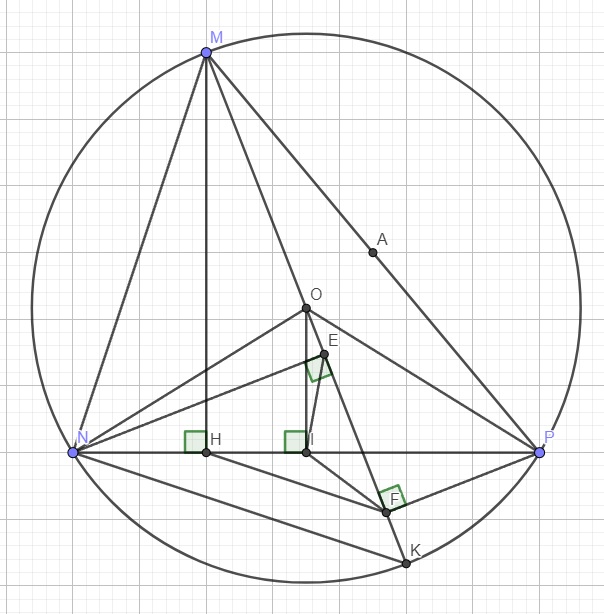
Bài 2: Cho tam giác MNP có ba góc nhọn nội tiếp đường tròn (O). Kẻ đường cao MH của tam giác MNP và đường kính MK của (O). Gọi F là chân đường vuông góc kẻ từ điểm P đến đường thẳng MK
a) C/m: tứ giác MHFP nội tiếp đường tròn
b) C/m: HF // NK
c) Lấy I là trung điểm của đoạn thẳng NP. Gọi E là chân đường vuông góc kẻ từ điểm N đến đường thẳng MK . C/m: góc IHF = góc IFH và I là tâm đường tròn ngoại tiếp của tam giác HEF
d) Biết góc MPN = 30 độ, MH = 3cm. Tính diện tích và thể tích hình tạo thành khi quay đường tròn ngoại tiếp tứ giác MHFP quanh cạnh MP
Bài 1:
Diện tích mặt cầu bằng 4 lần diện tích hình tròn lớn, bằng bốn lần hằng số Pi nhân với bình phương bán kính của hình cầu.
Công thức:
\(4\pi r^2\)
Với bán kính (r = 2) cm, ta tính được diện tích mặt cầu:
\(S=4\pi\cdot\left(2\right)^2=16\pi\) (cm2)
Thể tích hình cầu được tính bằng ba phần tư của Pi nhân với lập phương bán kính hình cầu.
Công thức:
\(V=\dfrac{4}{3}\pi r^3\)
Với bán kính (r = 2) cm, ta tính được thể tích hình cầu:
\(V=\dfrac{4}{3}\pi\cdot\left(2\right)^3=\dfrac{32}{3}\pi\) (cm3)
Bài 2:
a) Để chứng minh tứ giác MHFP nội tiếp đường tròn, ta cần chứng minh góc (MHP) bằng góc (MFP).
Vì (MH) là đường cao của tam giác (MNP), nên góc (MHP) vuông.
Góc (MFP) cũng vuông vì (MF) là đường cao của tứ giác (MHFP).
Do đó, tứ giác (MHFP) nội tiếp đường tròn.
b) Ta biết (HF) là đường cao của tam giác (MNP), và (NK) là đường kính của đường tròn ngoại tiếp tam giác (MNP).
Vì đường cao và đường kính cắt nhau tại tâm đường tròn, nên (HF) // (NK).
c) Ta biết (I) là trung điểm của đoạn thẳng (NP).
Góc (IHF) bằng góc (IFH) vì (HF) // (NK) (đã chứng minh ở bước b).
(I) là tâm đường tròn ngoại tiếp của tam giác (HEF) vì (I) nằm trên đường tròn ngoại tiếp tam giác (HEF).
d) Để tính diện tích và thể tích, ta cần biết góc (MPN) và chiều dài (MH).
Diện tích và thể tích hình tạo thành khi quay đường tròn ngoại tiếp tứ giác (MHFP) quanh cạnh (MP) có thể tính bằng công thức của hình tròn và hình trụ.
1.
\(S=4\pi R^2=4.\pi.2^2=16\pi\left(cm^2\right)\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi.2^3=\dfrac{32\pi}{3}\left(cm^3\right)\)
2.
a.
Theo giả thiết ta có \(\widehat{MHP}=\widehat{MFP}=90^0\)
\(\Rightarrow H,F\) cùng nhìn MP dưới 1 góc vuông nên MHFP nội tiếp
b.
Từ câu a, do MHFP nội tiếp \(\Rightarrow\widehat{HFM}=\widehat{HPM}\) (cùng chắn HM)
Lại có \(\widehat{HPM}=\widehat{NKM}\) (cùng chắn MN của (O))
\(\Rightarrow\widehat{HFM}=\widehat{NKM}\)
\(\Rightarrow HF||NK\) (hai góc đồng vị bằng nhau)
c.
Ta có: \(\widehat{PMK}=\widehat{PNK}\) (cùng chắn PK của (O))
\(\widehat{PNK}=\widehat{IHF}\) (đồng vị)
Mà \(OM=OP=R\Rightarrow\widehat{PMK}=\widehat{OPM}\) (2 góc đáy của tam giác cân OMP)
\(\Rightarrow\widehat{IHF}=\widehat{OPM}\) (1)
I là trung điểm NP \(\Rightarrow OI\perp NP\Rightarrow\widehat{OIP}=90^0\)
\(\Rightarrow I,F\) cùng nhìn OP dưới 1 góc vuông nên OIFP nội tiếp
\(\Rightarrow\widehat{OFI}=\widehat{OPI}\) (cùng chắn OI) (2)
Cũng từ câu a MHFP nội tiếp \(\Rightarrow\widehat{MPH}=\widehat{MFH}\)
\(\Rightarrow\widehat{OPM}+\widehat{OPI}=\widehat{OFI}+\widehat{IFH}\) (3)
(2);(3) \(\Rightarrow\widehat{OPM}=\widehat{IFH}\) (4)
(1);(4) \(\Rightarrow\widehat{IHF}=\widehat{IFH}\)
\(\Rightarrow\Delta IHF\) cân tại I \(\Rightarrow IH=IF\) (5)
Do I và E cùng nhìn ON dưới 1 góc vuông \(\Rightarrow ONIE\) nội tiếp
\(\Rightarrow\widehat{NEI}=\widehat{NOI}\)
Mà \(\widehat{NOI}=\widehat{POI}\) (ONP cân tại O nên OI vừa là trung tuyến vừa là phân giác)
Tam giác OPI vuông tại I \(\Rightarrow\widehat{POI}+\widehat{OPI}=90^0\)
\(\Rightarrow\widehat{NEI}+\widehat{OPI}=90^0\)
Mà từ (2): \(\widehat{OPI}=\widehat{OFI}\) \(\Rightarrow\widehat{NEI}+\widehat{OFI}=90^0\)
Mặt khác \(\widehat{NEI}+\widehat{IEF}=\widehat{NEF}=90^0\)
\(\Rightarrow\widehat{IEF}=\widehat{OFI}\)
\(\Rightarrow\Delta IEF\) cân tại I \(\Rightarrow IE=IF\) (6)
(5);(6) \(\Rightarrow IH=IE=IF\) hay I là tâm đường tròn ngoại tiếp tam giác HEF
d.
Trong tam giác vuông MPH ta có:
\(sin\widehat{MPN}=\dfrac{MH}{MP}\Rightarrow MP=\dfrac{MH}{sin\widehat{MPN}}=\dfrac{3}{sin30^0}=6\left(cm\right)\)
H, F cùng nhìn MP dưới 1 góc vuông nên tâm đường tròn ngoại tiếp MHFP có tâm A là trung điểm MP
\(\Rightarrow\) Bán kính đường tròn là \(r=\dfrac{MP}{2}=3\left(cm\right)\)
Khi quay đường tròn quanh đường kính MP ta sẽ được 1 mặt cầu tâm A bán kính \(r=3\left(cm\right)\)
Diện tích mặt cầu là:
\(S=4\pi r^2=36\pi\left(cm^2\right)\)
Thể tích hình cầu là:
\(V=\dfrac{4}{3}\pi r^3=36\pi\left(cm^3\right)\)