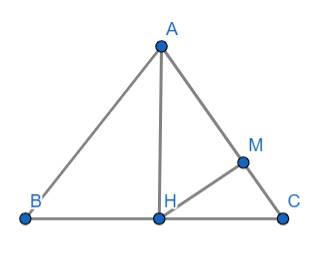
AH là đường cao mà tam giác ABC là tam giác đều nên AH đồng thời là đương trung tuyến
\(\Rightarrow H\) là trung điểm của BC
\(\Rightarrow HB=HC=\dfrac{BC}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AH=\sqrt{\dfrac{AB^2AC^2}{AB^2+AC^2}}=\sqrt{\dfrac{7^2\cdot7^2}{7^2+7^2}}=\dfrac{7\sqrt{2}}{2}\left(cm\right)\)
Xét tam giác AHC có HM là đường cao ta có:
\(\dfrac{1}{HM^2}=\dfrac{1}{AH^2}+\dfrac{1}{HC^2}\)
\(\Rightarrow HM=\sqrt{\dfrac{AH^2HC^2}{AH^2+HC^2}}=\sqrt{\dfrac{\left(\dfrac{7\sqrt{2}}{2}\right)^2\cdot3,5^2}{\dfrac{7\sqrt{2}}{2}+3,5}}=\dfrac{7\sqrt{6}}{6}\left(cm\right)\)
Xét tam giác AHM vuông tại M áp dụng định lý Py-ta-go ta có:
\(AH^2=HM^2+AM^2\)
\(\Rightarrow AM=\sqrt{AH^2-HM^2}=\sqrt{\left(\dfrac{7\sqrt{2}}{2}\right)^2-\left(\dfrac{7\sqrt{6}}{6}\right)^2}=\dfrac{7\sqrt{3}}{3}\left(cm\right)\)
Mà: \(AM+MC=AC\)
\(\Rightarrow MC=AC-AM=7-\dfrac{7\sqrt{3}}{3}=\dfrac{21-7\sqrt[]{3}}{3}\)













