6.
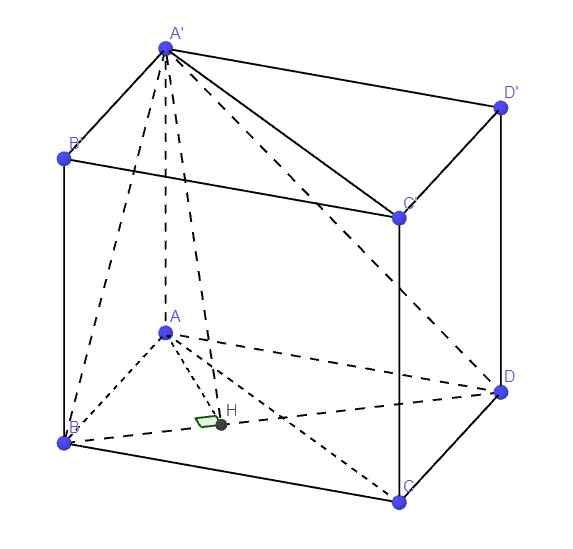
Do \(AA'\perp\left(ABCD\right)\) (t/c hình hộp chữ nhật)
Mà \(AA'\in\left(ACC'A'\right)\)
\(\Rightarrow\left(ACC'A'\right)\perp\left(ABCD\right)\Rightarrow\) góc giữa (ACC'A') avf (ABCD) bằng 90 độ
b.
Từ H kẻ AH vuông góc BD (H thuộc BD)
Do \(AA'\perp\left(ABCD\right)\Rightarrow AA'\perp BD\)
\(\Rightarrow BD\perp\left(A'AH\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BD\perp AH\\BD\perp A'H\end{matrix}\right.\)
Mà \(BD=\left(A'BD\right)\cap\left(ABCD\right)\Rightarrow\widehat{AHA'}\) là góc giữa (A'BD) và (ABCD)
\(AH=\dfrac{AB.AD}{\sqrt{AB^2+AD^2}}=\dfrac{bc}{\sqrt{b^2+c^2}}\)
\(\Rightarrow tan\widehat{AHA'}=\dfrac{AA'}{AH}=\dfrac{a\sqrt{b^2+c^2}}{bc}\)
7.
Kẻ \(AI\perp CM\Rightarrow\widehat{IAM}=\widehat{BCM}\) (góc có cạnh tương ứng vuông góc)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{BC^2+\left(\dfrac{AB}{2}\right)^2}=2a\)
\(\Rightarrow AI=AM.cos\widehat{IAM}=\dfrac{AB}{2}.cos\widehat{BCM}=\dfrac{AB}{2}.\dfrac{BC}{CM}=\dfrac{a\sqrt{3}}{2}\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp CI\\CI\perp AI\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CI\perp\left(SAI\right)\Rightarrow\left\{{}\begin{matrix}CI\perp SI\\CI\perp AI\end{matrix}\right.\)
Mà \(CI=\left(SMC\right)\cap\left(ABC\right)\Rightarrow\widehat{SIA}\) là góc giữa (SMC) và (ABC)
\(tan\widehat{SIA}=\dfrac{SA}{AI}=\dfrac{4\sqrt{3}}{3}\Rightarrow\widehat{SIA}\approx66^035'\)